课程地址

https://www.bilibili.com/video/BV1Eb411W7kc?p=2

思维导图

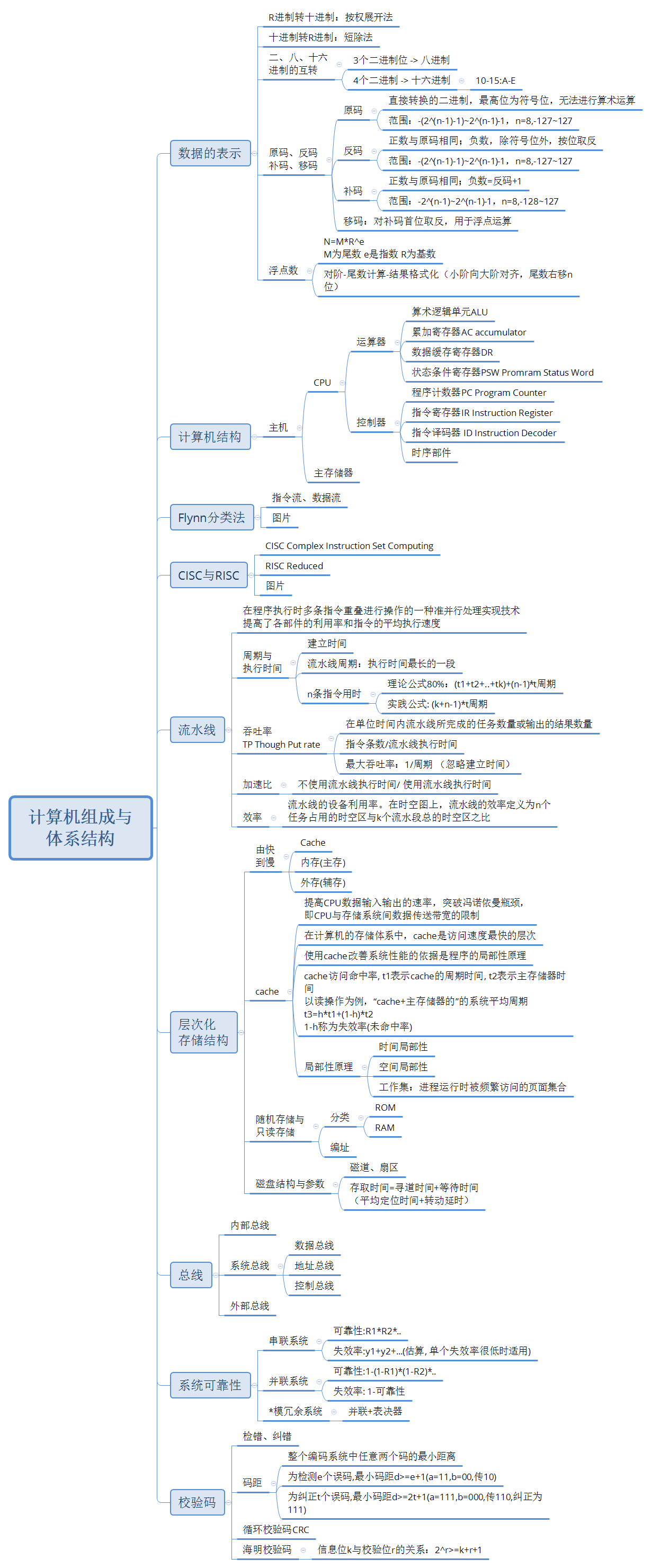
计算机组成与体系结构

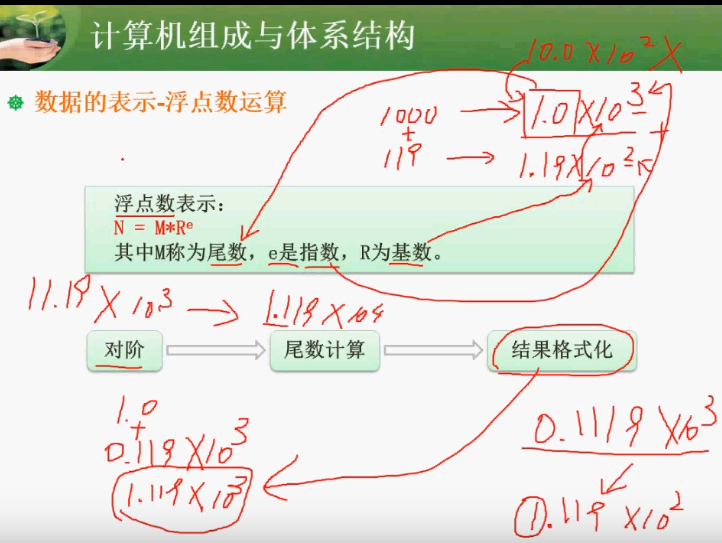
• 数据的表示
• 计算机结构
• Flynn分类法
• CISC与RISC
• 流水线
• 层次化存储结构
• 总线
• 系统可靠性
• 校验码

数据的表示

• R进制转十进制

• 十进制转R进制

• 码制

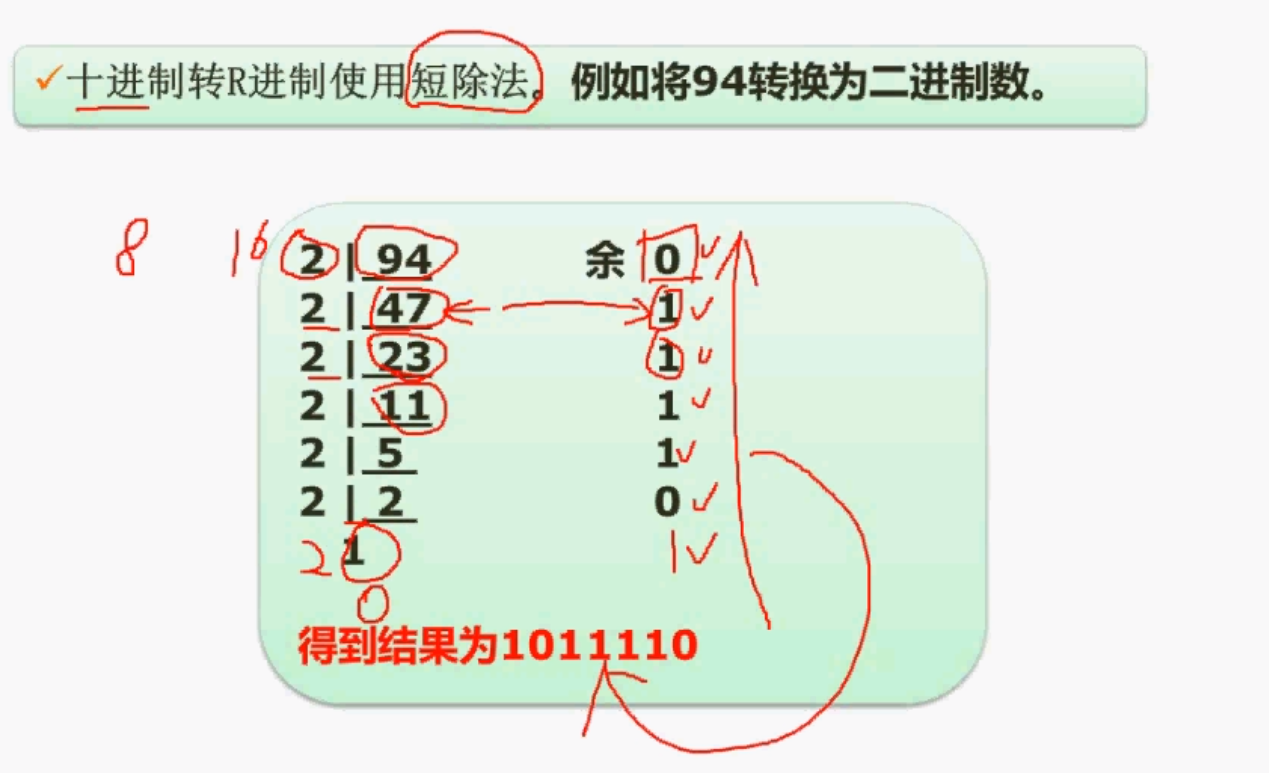
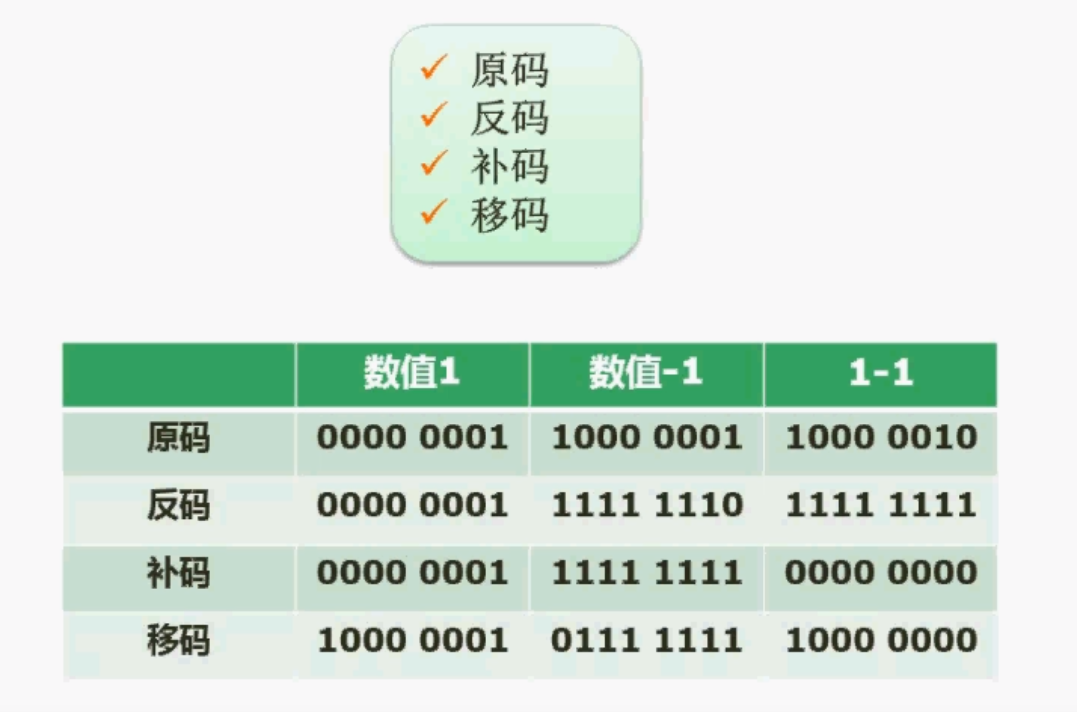
• 原码
  
  最高位为符号位（正0负1），其余位为绝对值，区分+0和-0

• 反码
  
  最高位为符号位（正0负1），其余位为绝对值取反（原码除符号位外取反），区分+0和-0

• 补码
  
  最高位为符号位（正0负1），反码基础上加1，不区分+0和-0

• 移码
  
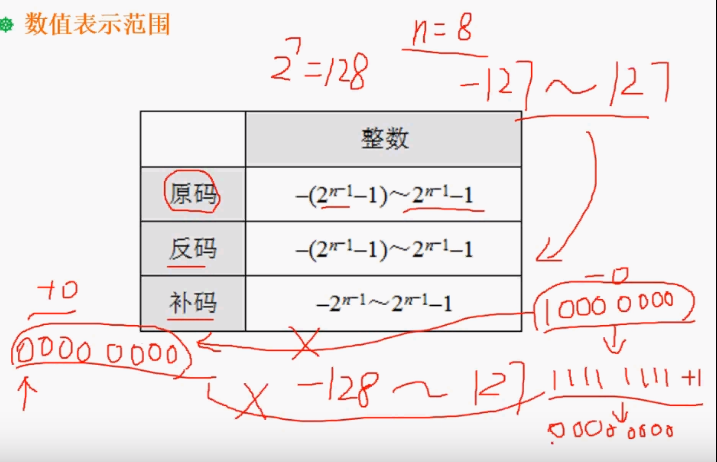
  在偏移2^n-1的情况下，补码符号位取反即为移码

• 数值表示范围

• 浮点数运算

  对大阶—>尾数计算—>结果格式化（小数点前只能有一位数字）

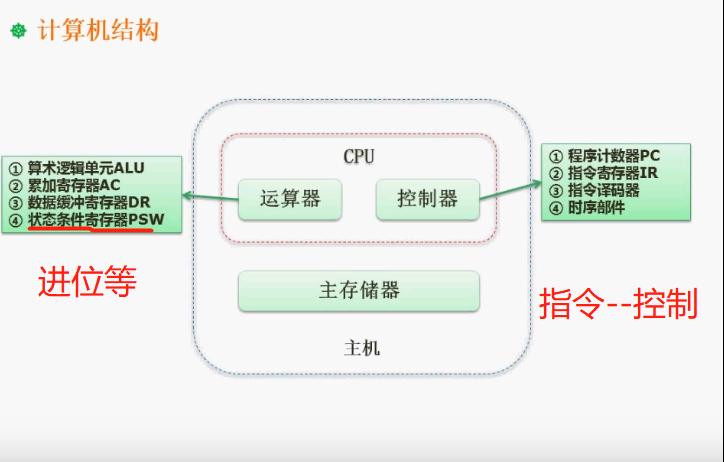
计算机结构

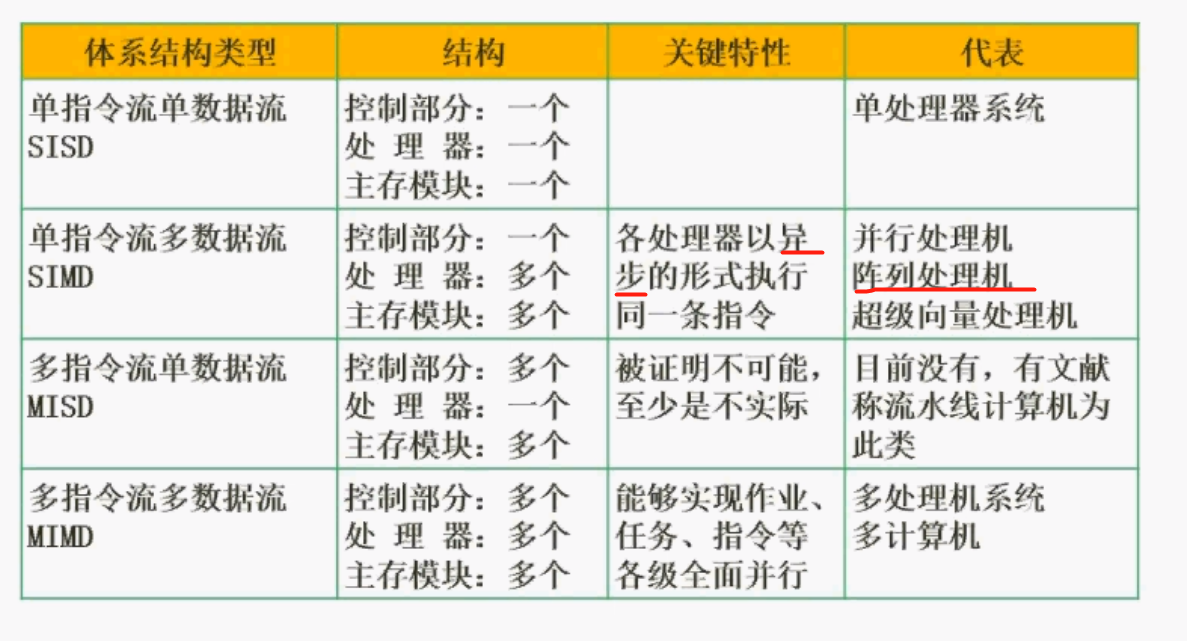
Flynn分类法

S:单
M:多
I:指令流
D:数据流
MISD:多指令流单数据流不切实际

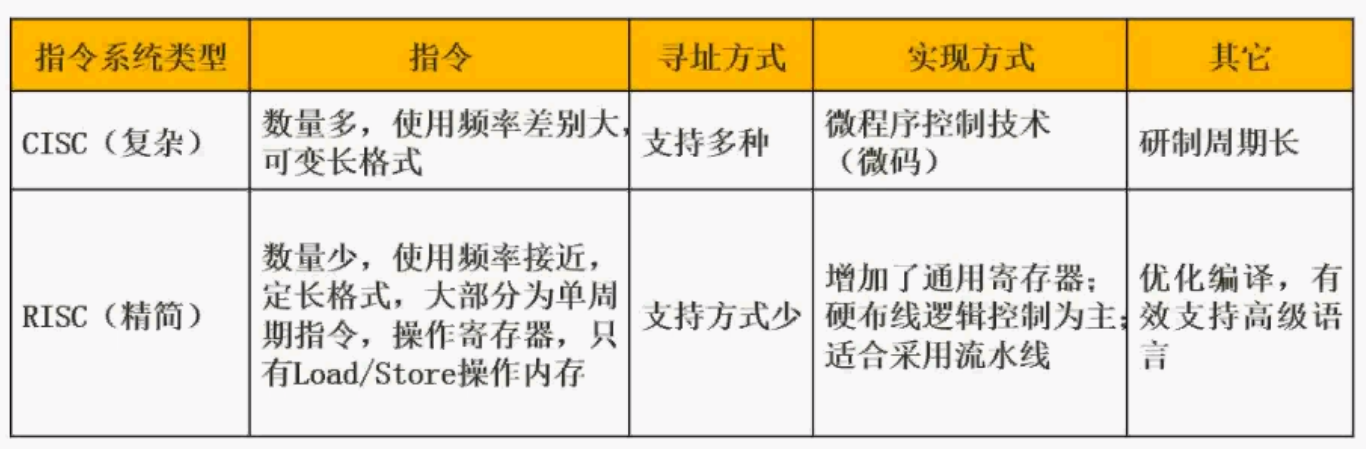
CISC与RISC

CISC时间较早,用于定制化计算机（如天气预报计算机）数量较多,使用频率差别大,可变长格式,生产周期长,寻址种类多

RISC可视为当代计算机,大部分操作针对寄存器操作,只有Load/Store操作内存, 数量较少（计算机通用）,使用频率差别小,定长格式,流水线生产,寻址种类少

流水线

流水线是指在程序执行时多条指令重叠操作的一种准并行处理实现技术。各个部件同时处理是针对不用指令而言的,它们可同时为多条指令的不同部分进行工作，以提高各部件的利用率和指令的平均执行速度。

• 流水线计算

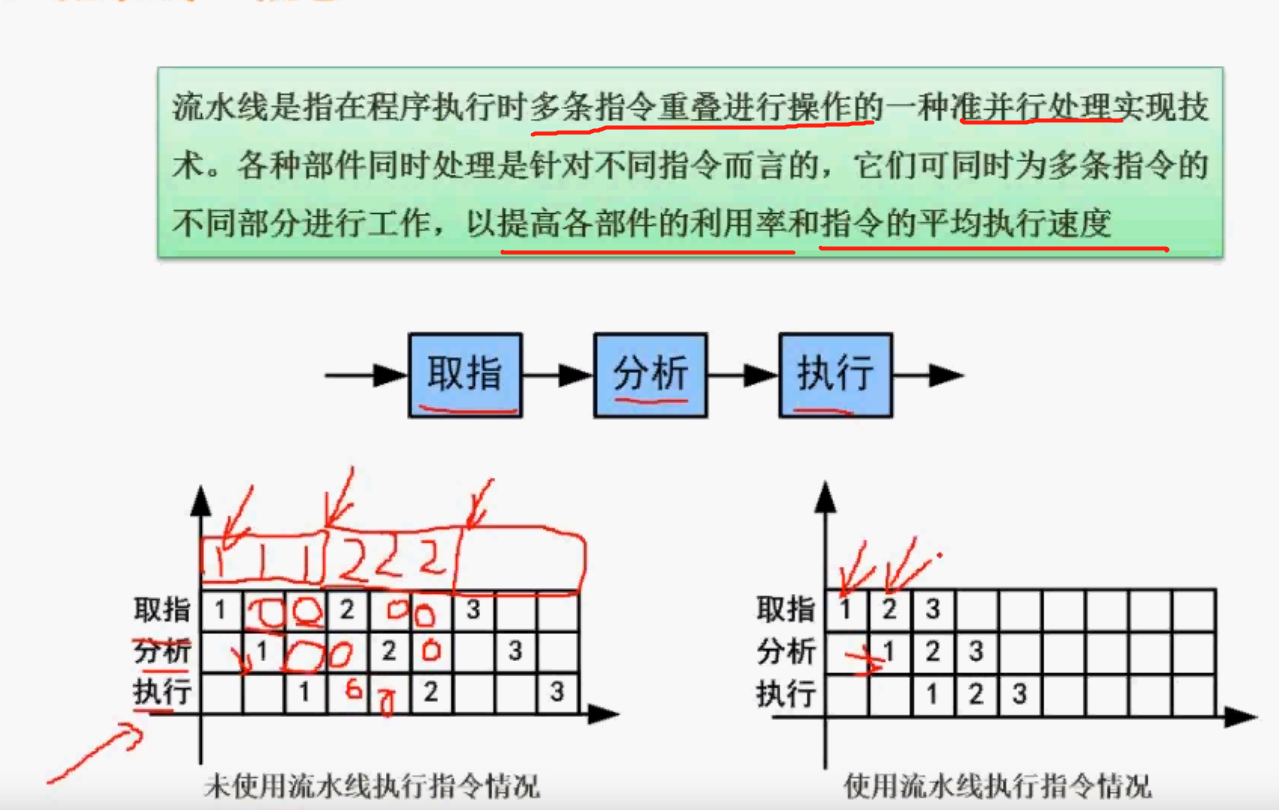
• 流水线周期为执行时间最长的一段

• 流水线执行时间计算

  例题：若指令流水线把一条指令分为取指、分析和执行三部分，且三部分的时间分别是t取指=2ns ，t分析=2ns，t执行=1ns。则100条指令全部执行完毕需多少时间?

  计算公式：1条指令执行时间 + （指令条数 - 1）* 流水线周期

  1. 理论公式计算 (80%，优先使用)

     (t1 + t2 + … + tk) + (n - 1) * ▲t，
     即：(2+2+1) + (100-1) * 2 = 5 + 198 = 203

  2. 实践公式计算 (20%)

     (k + n - 1) * ▲t，其中k为一条指令分成的段数，
     即：(3 + 100 - 1) * 2 = 102 * 2 =204

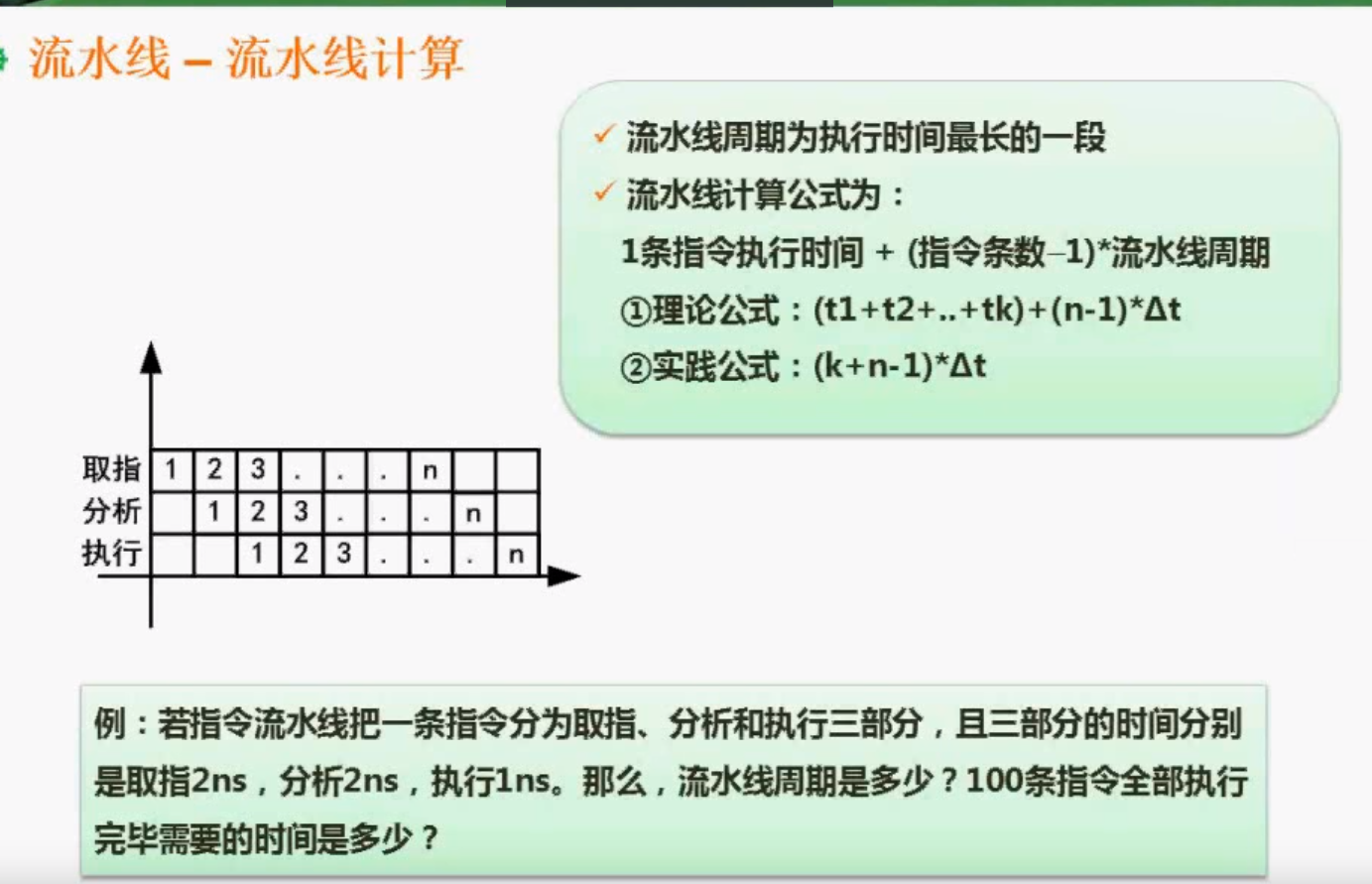
• 流水线吞吐率计算

• 流水线加速比计算

• 流水线的效率

  阴影面积 / 总面积 = 流水线的效率

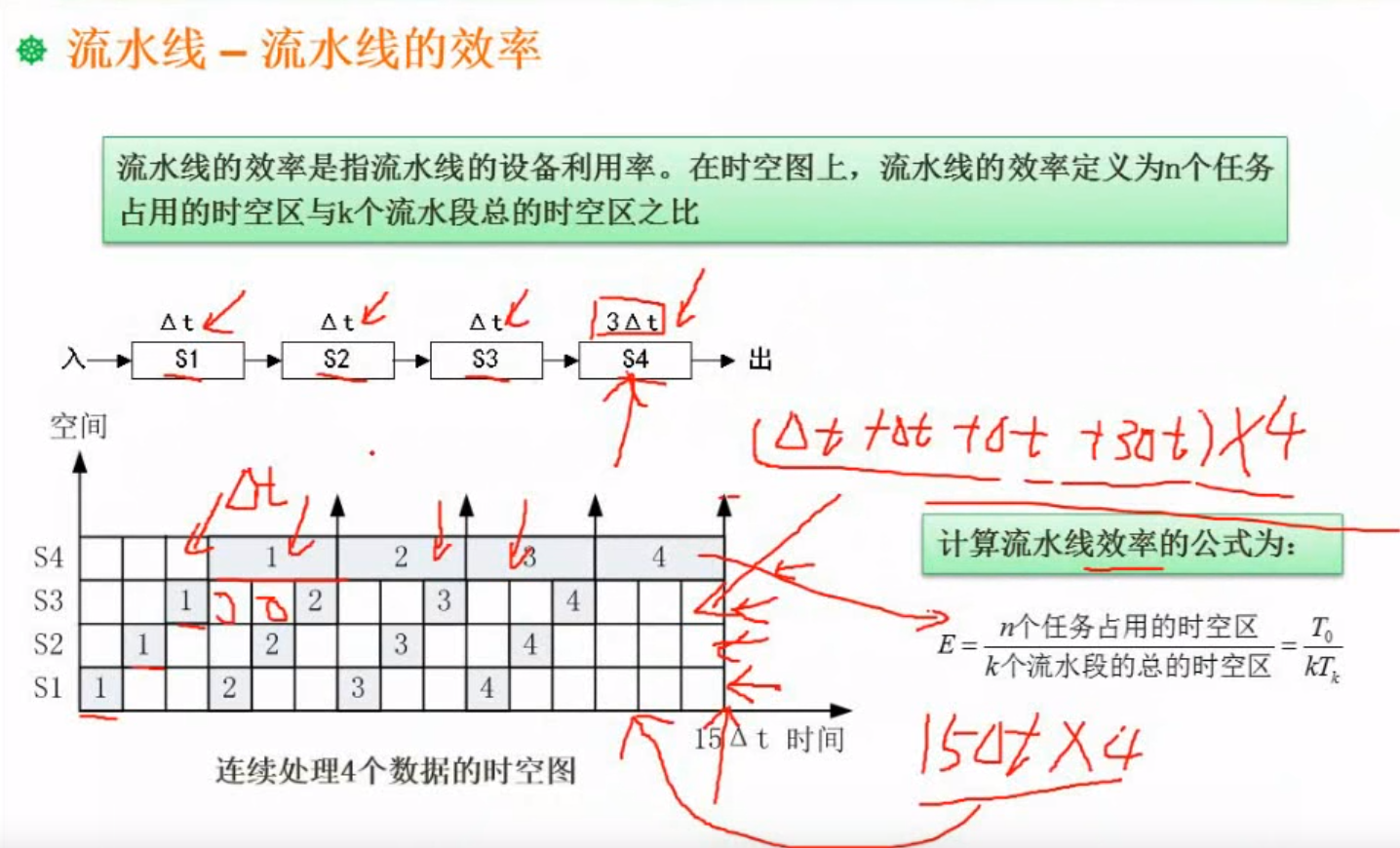
层次化存储结构

• Cache概念

  CPU向cache查找想要访问的数据中,当存在称为命中；当不存在则称为未命中，改为从主存中调取数据，并存放入Cache中

• 局部性原理

  局部性原理是指计算机在执行某个程序时，倾向于使用最近使用的数据。局部性原理有两种表现形式：时间局部性和空间局部性。

  时间局部性是指被引用过的存储器位置很可能会被再次引用，例如：重复的引用一个变量时则表现出较好的时间局部性

  空间局部性是指被引用过的存储器位置附近的数据很可能将被引用；例如：遍历二维数组时按行序访问数据元素具有较好的空间局部性

• 主存分类

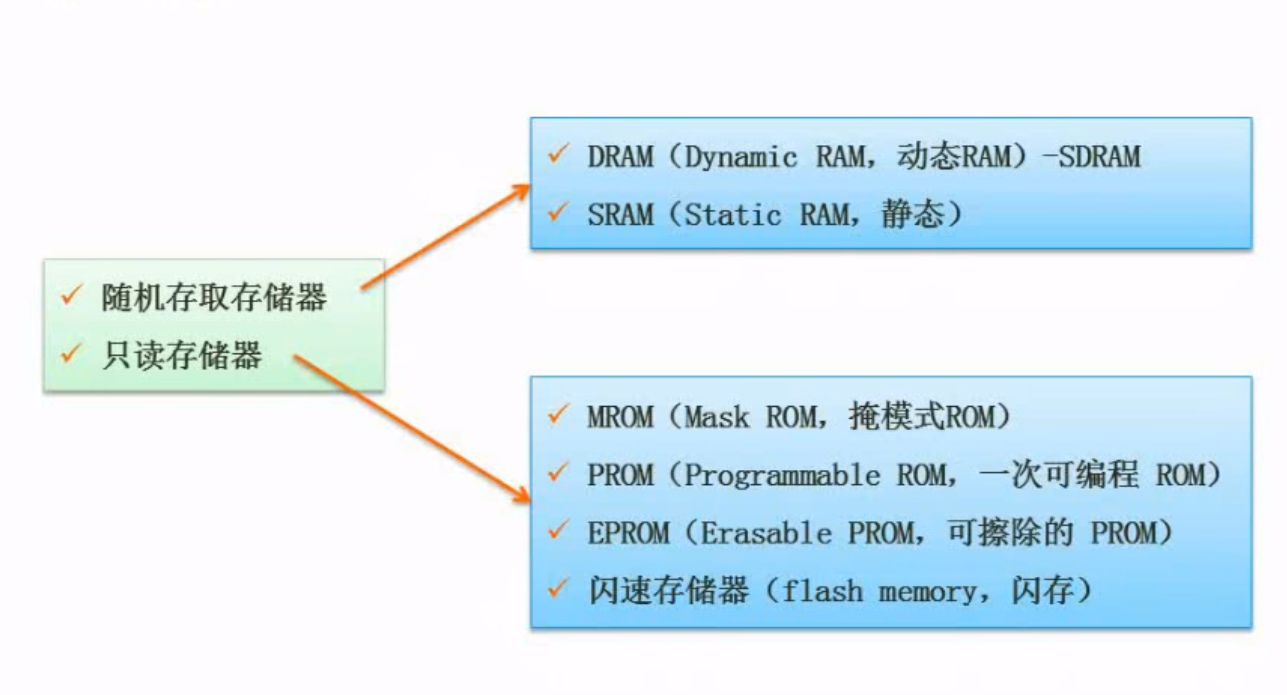
• 主存编址

  例题：内存地址从AC000H到C7FFFH，共有（1）K个地址单元，如果该内存地址按字（16bit）编址，由28片存储器芯片构成。已知构成此内存的芯片每片有16K个存储单元，则该芯片每个存储单元存储（2）位。

  解答：
  
  1.C7FFFH - AC000H + 1 -> C8000H - AC000H = 1C000H -> 1C000H / 2¹⁰ = 1 * 16⁴ + 12 * 16³ / 2¹⁰ = 1 * 2¹⁶ + 12 * 2¹² / 2¹⁰ = 2⁶ + 12 * 2² = 112K个地址单元
  
  2.(112K * 16bit) / (28 * 16K * X) = 1 -> X = (112K * 16bit) / (28 * 16K) = 4bit

• 磁盘结构与参数

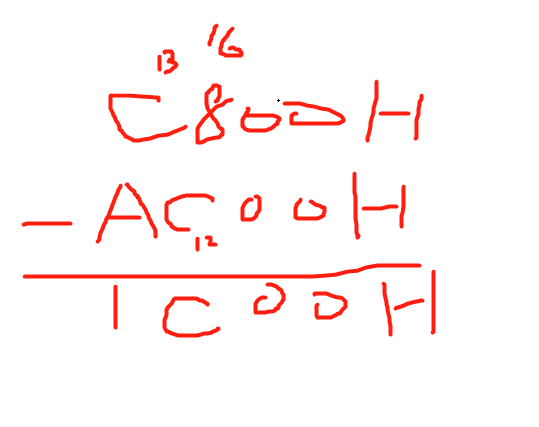
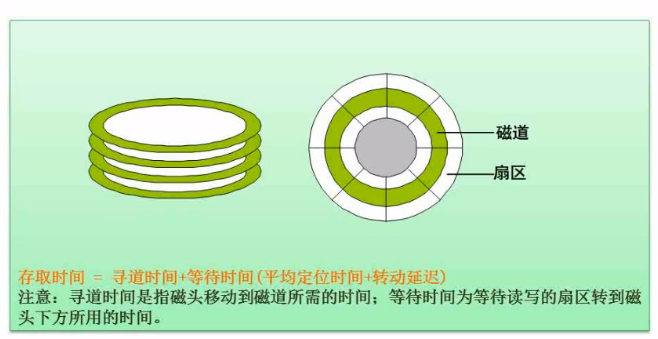
存取时间 = 寻道时间（平均定位时间） + 等待时间（转动延时）

例题（较难）：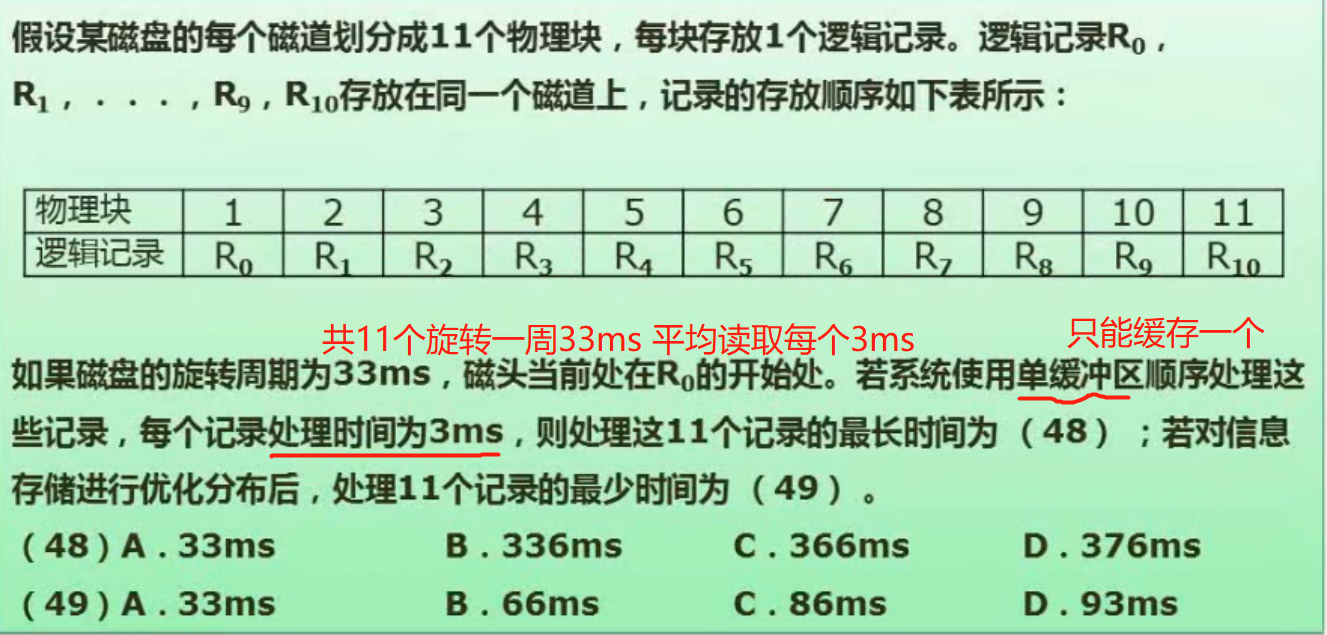

解答：

1. 最长时间 = 处理R0需要的时间（首次直接访问） + 处理其他块需要的时间（需要转动最长的时间） -> 6 + (30 + 6) * 10 = 366ms

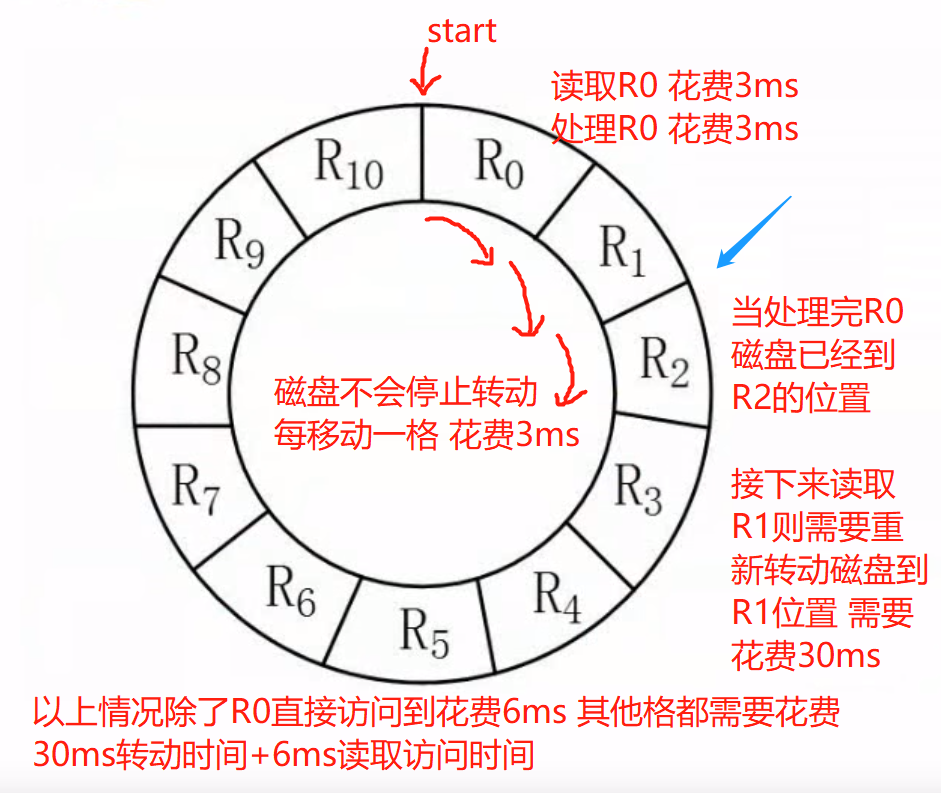
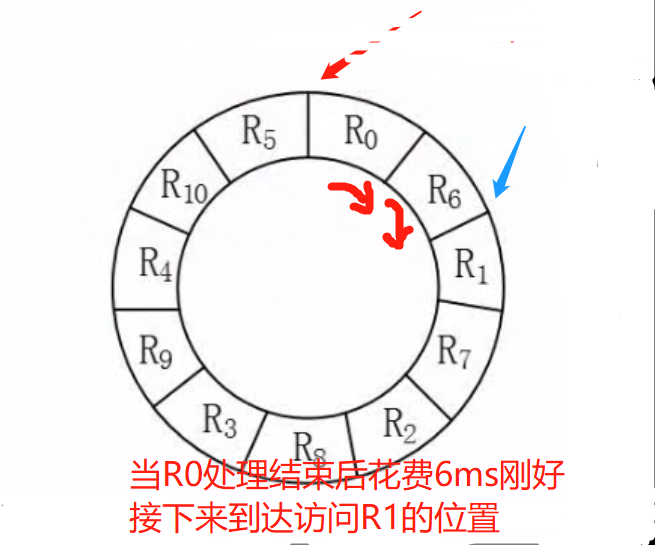
2. 最少时间：没有时间浪费，不需要转动-> 6 * 11 = 66ms

总线（选择题，基本概念）

总线：内部总线，系统总线，外部总线

系统总线：数据总线，地址总线，控制总线

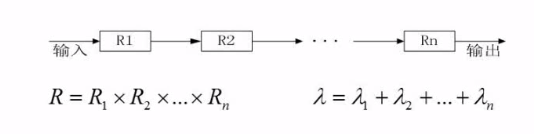
系统可靠性

• 串联系统

  R代表可靠率，串联系统可靠性通过相乘得到结果，即：系统可靠率R = 子系统1的可靠率R1 * 子系统2的可靠率R2 * … * 子系统n的可靠率Rn

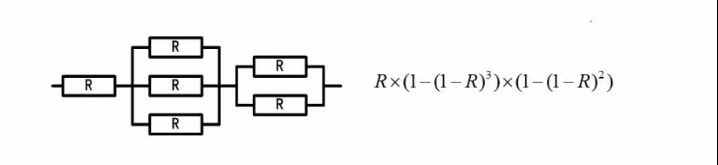
• 并联系统

  R代表可靠率，并联系统可靠性通过计算1 - 子系统同时失效的概率得到。因为该系统只要有一条路能通便可用，只有全部不通，系统才失效。即：系统可靠率R = 1 - （子系统1的失效率（1-R1） * (子系统2的失效率（1-R2） * … * (子系统n的失效率（1-Rn））

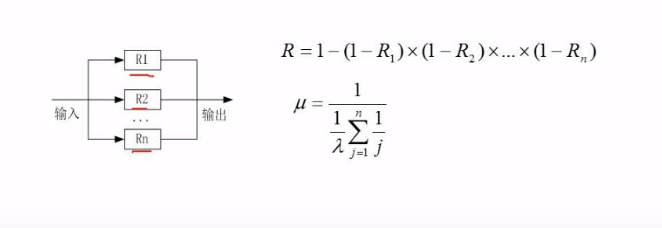
例题

下图中总体为串联系统，局部并联系统

差错控制（基本必考）

• 码距：整个编码系统中任意两个码字的最小距离

• 检错和纠错

  在一个码组内为了检测e个误码，最小码距d应满足d >= e + 1，例：2位长度的二进制编码（a=11，b=00，传10）
  
  在一个码组内为了纠正t个误码，最小码距d应满足d >= 2t + 1，例：3位长度的二进制编码（a=111，b=000，传110，纠正为111）

• 循环校验码CRC（可以检错不能纠错）

  参考：CRC校验原理及步骤

  CRC校验码计算例题：
  
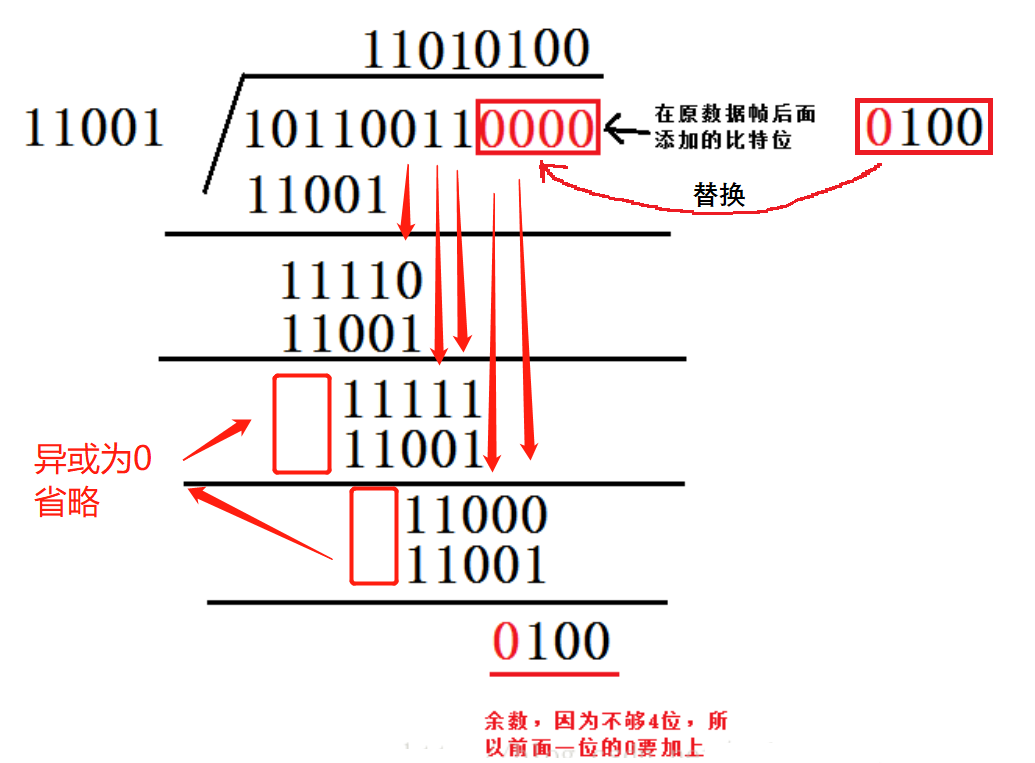
  原始报文为“10110011”，其生成多项式为“X⁴ + X³ + 1”。对其进行CRC编码后的结果为？

  具体计算过程：
  
  1、将生成多项式转化为二进制序列：X⁴ + X³ + 1 -> 11001
  
  2、多项式的位数为5，则在数据帧的后面加上5-1位0（余数的位数），数据帧变为101100110000，然后使用模2除法除以除数11001，得到余数。
  
  3、将计算出来的4位余数替换第2步中添加的5-1位0，得到CRC编码后的结果101100110100。

  检错：
  
  发送端将CRC编码后的数据帧发送给接收端，接收端收到数据帧后，用上面选定的生成多项式，做模2除法运算，验证余数是否为0，如果为0，则说明数据帧没有出错。

• 海明校验码

  参考：海明校验码

  海明校验法中，校验码存放在2ⁿ位置，存在公式2^r ≥ k + r + 1，则能正确生成海明校验码。其中r为校验位个数，k为信息位个数，信息位个数是已知的。

  海明校验码计算例题：
  
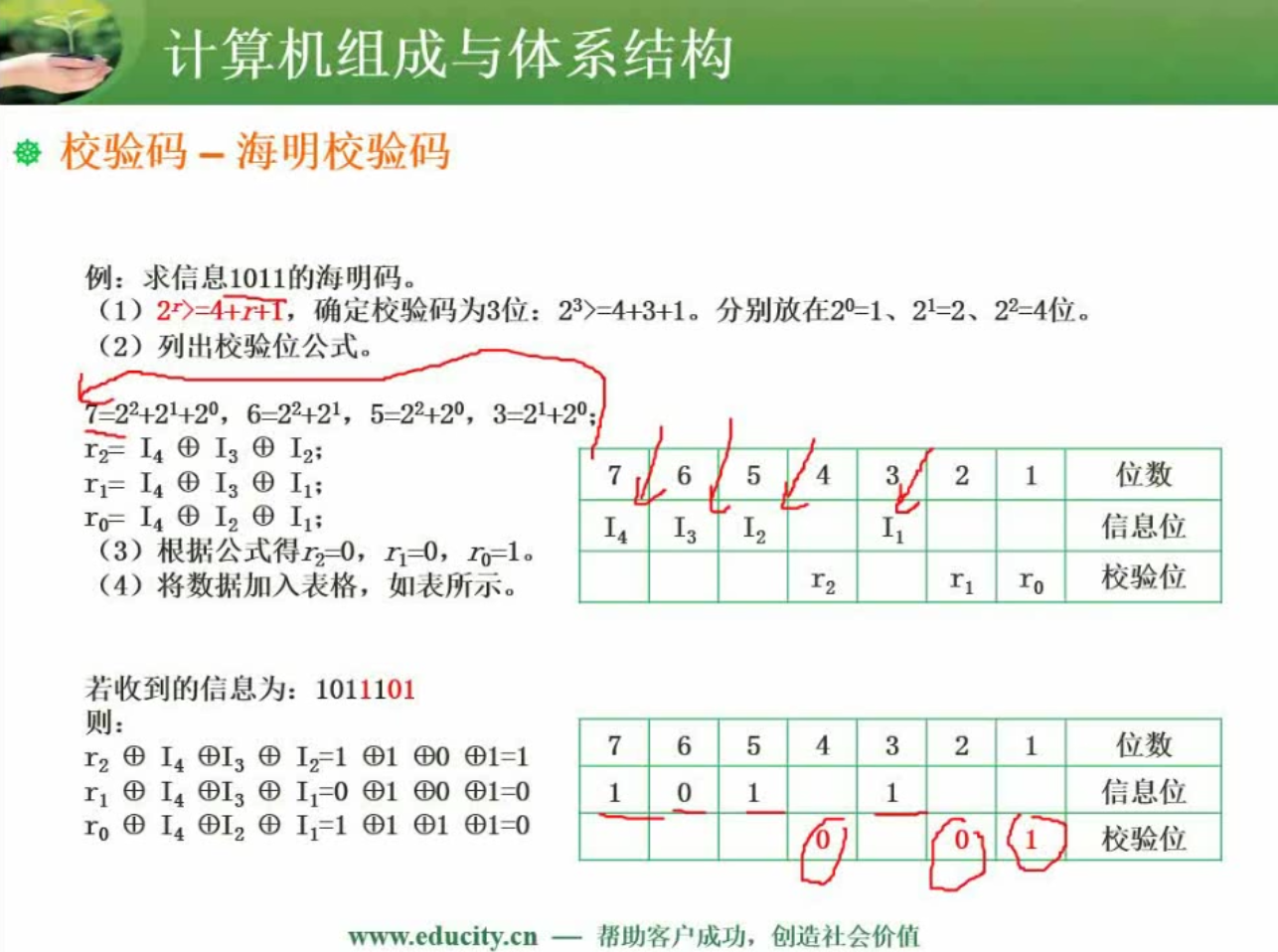
  求信息1011的海明码
  
  具体计算过程：
  
  1、首先确定信息位个数k为4，那么随之校验位的个数r也就知道了是3，画表格；
  
  2、根据信息位的位置列出校验位公式；
  
  3、根据公式得到校验位的值；
  
  4、将数据加入表格得到的结果就是信息的海明码。

  检错及纠错：
  
  将收到的校验位和第3步中产生的校验位做异或运算，运算的结果如果为全0，则说明数据帧没有出错，否则结果对应的10进制值为出错的位置。