课程地址

https://www.bilibili.com/video/BV1Eb411W7kc?p=80

思维导图

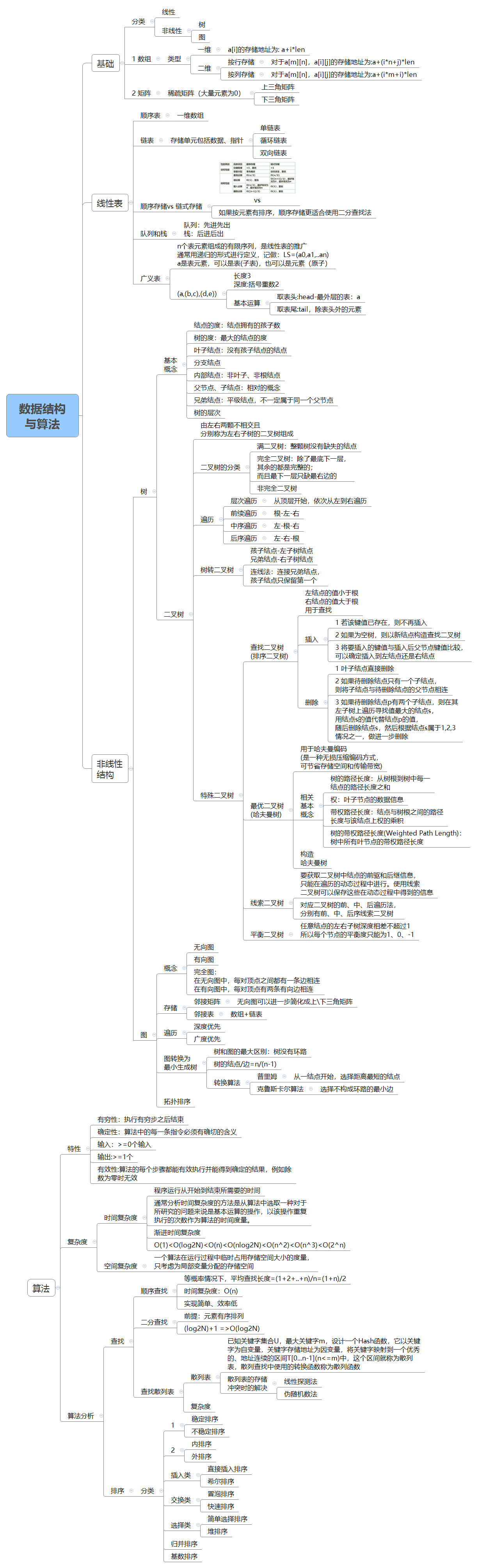
数据结构与算法基础（非常重要）

• 数组与矩阵
• 线性表（必考）
• 广义表
• 树与二叉树（必考）
• 图
• 排序与查找（重要）
• 算法基础及常见的算法

数组与矩阵

数组

稀疏矩阵

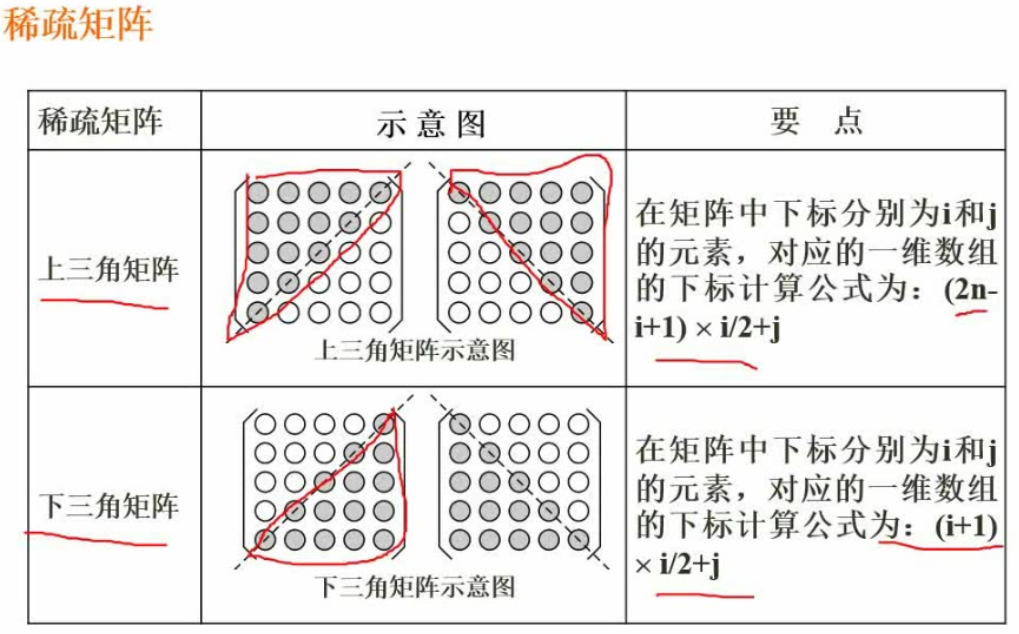
解题技巧：代入法（A_0,0, A_1,1）

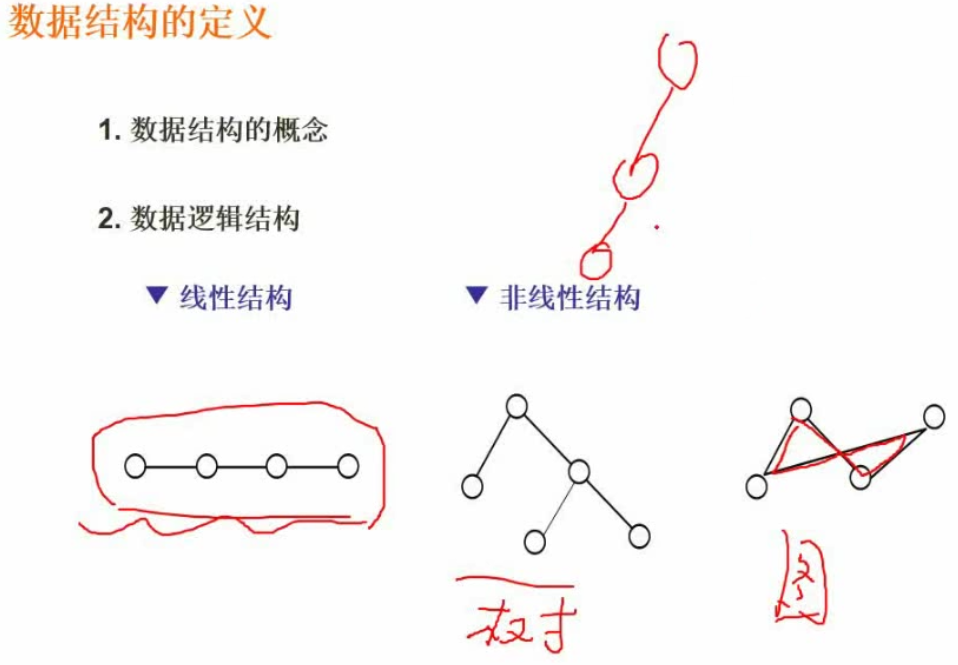
数据结构的定义

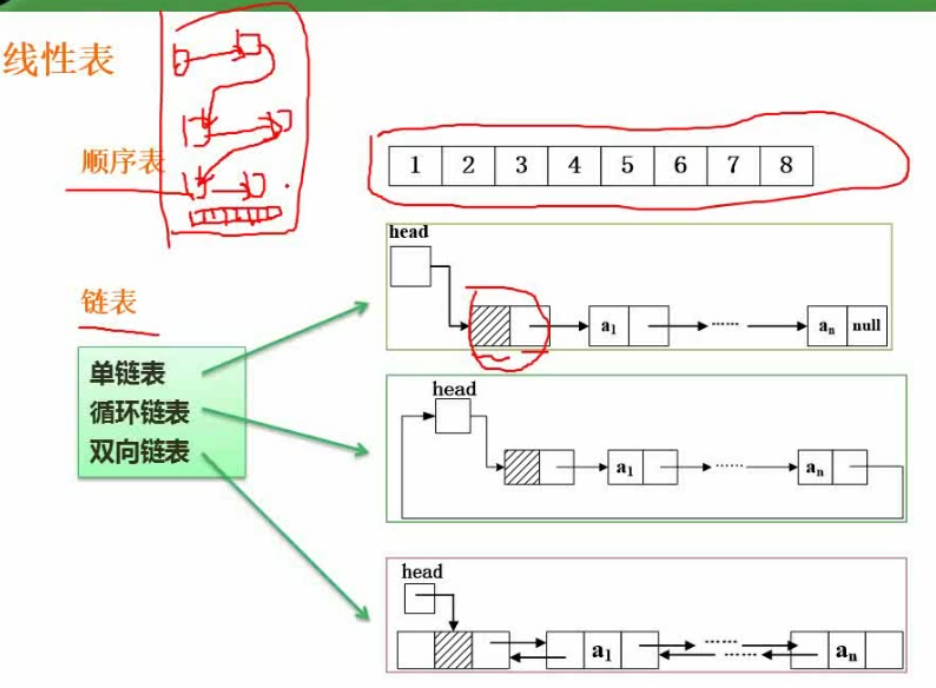
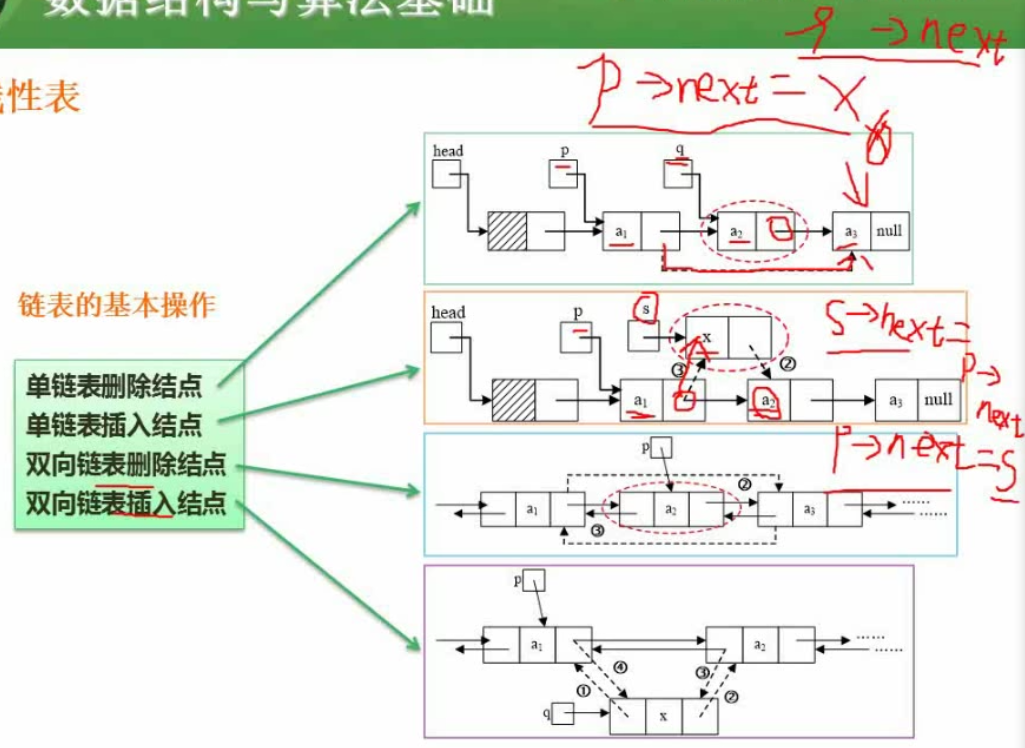
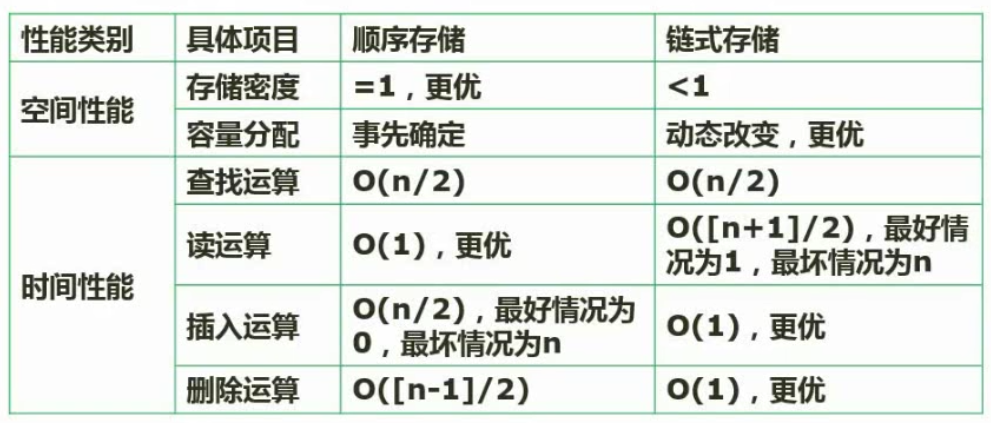
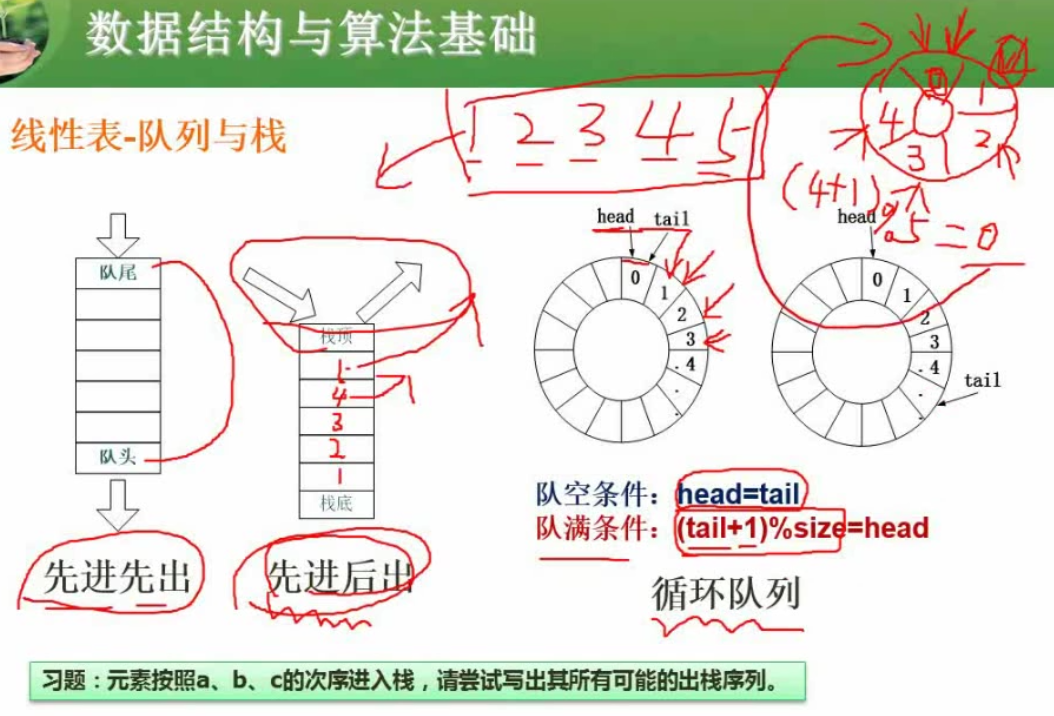
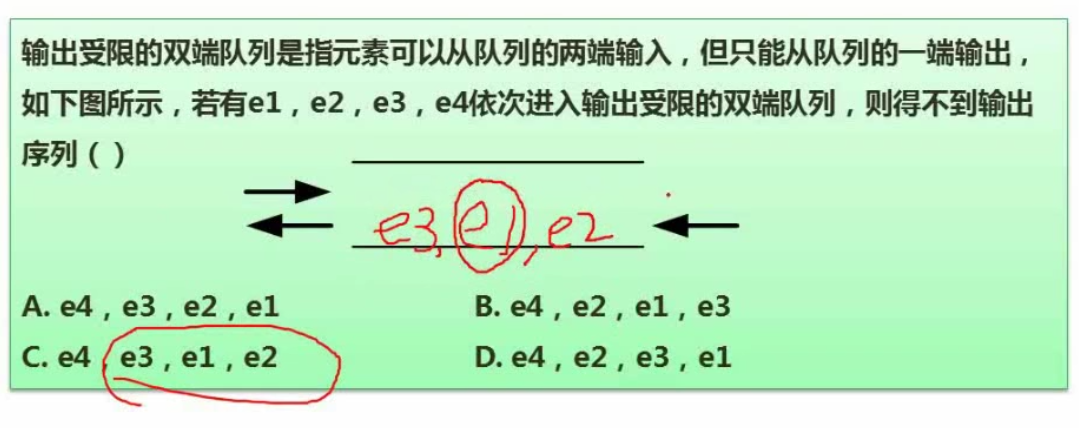
线性表（必考）

• 线性表常见存储结构

• 链表的基本操作

• 顺序存储与链式存储比较

• 队列与栈（重要，必考）

  避免对满条件与对空条件一致：少存一个

广义表

长度：最外层的表包含的元素个数

深度：嵌套的次数，包含括号的层数

表头：第一个表元素，head()操作

表尾：除第一个元素外的其他所有元素，tail()操作

数与二叉树（必考）

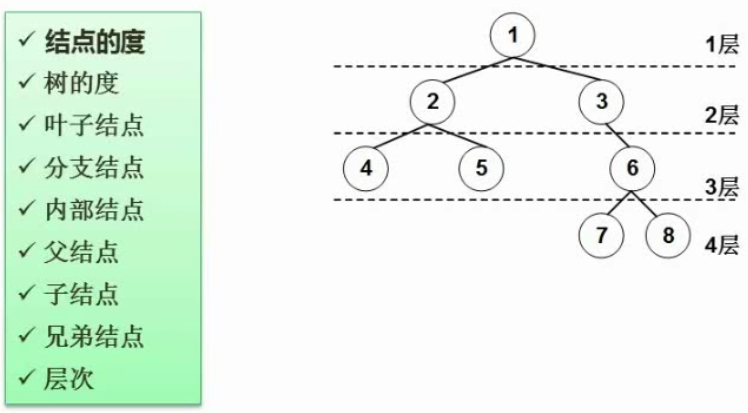
结点的度：拥有的孩子结点数

树的度：所有结点的度的最大值

叶子结点：没有孩子结点的结点

分支结点

内部结点：非叶子结点，也非根结点

父结点、子结点：相对概念

兄弟结点：平级结点，不一定属于同一个父结点

层次

• 二叉树的分类及重要特性

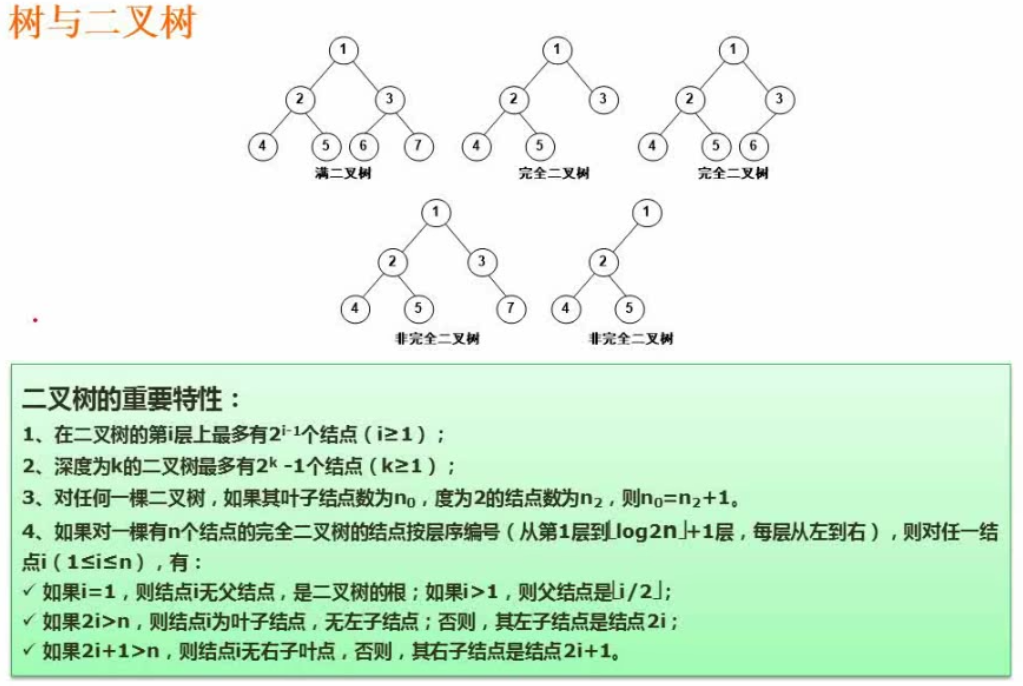
完全二叉树：除了最下层，其余是完整的；且最下一层从左到右依次排列，只缺最右边的

• 二叉树的遍历

  • 层次遍历：从顶层开始，从左到右 1 2 3 4 5 6 7 8

  • 前序遍历：根结点->左子结点->右子结点 1 2 4 5 7 8 3 6

  • 中序遍历：左子结点->根结点->右子结点 4 2 7 8 5 1 3 6

  • 后序遍历：左子结点->右子结点->根结点 4 8 7 5 2 6 3 1

• 反向构造二叉树

• 树转二叉树

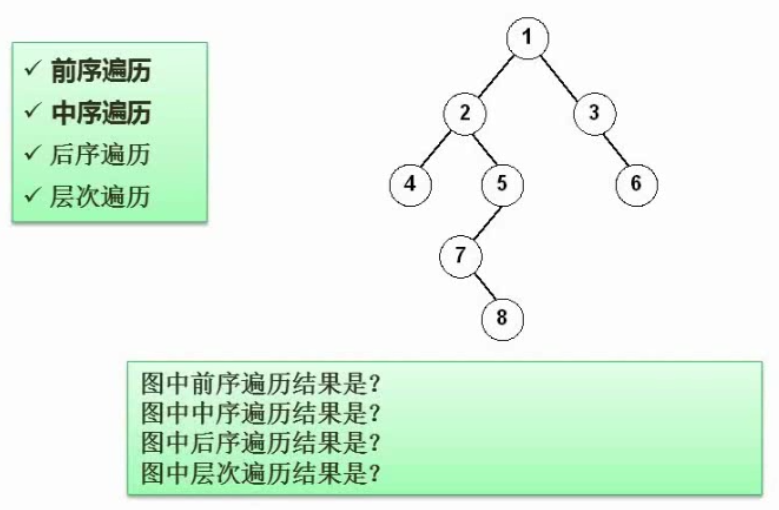
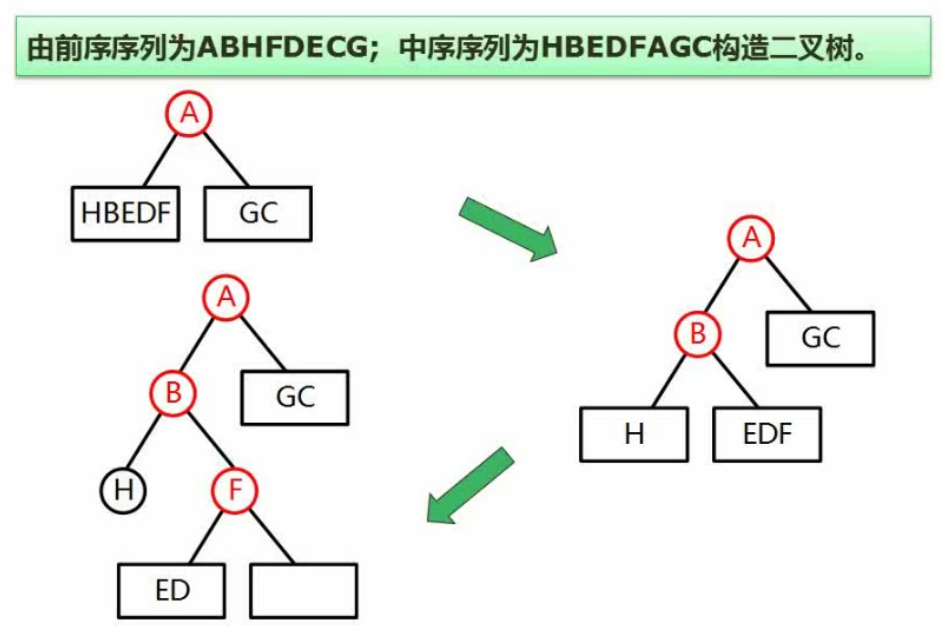
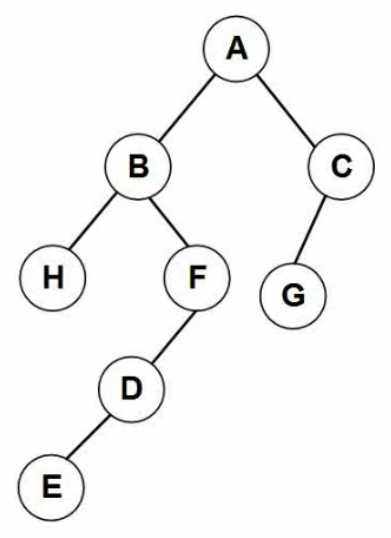
孩子结点->左子树结点

兄弟节点->右孩子结点

简化->连线法：连接兄弟结点，孩子结点只保留第一个，变形

• 查找二叉树（排序二叉树）

左孩子的值小于根，右孩子的值大于根

• 最优二叉树（哈夫曼树）

  基本概念：

  • 树的路径长度：从树根到树中每一结点的路径长度之和

  • 权：叶子结点的数据信息

  • 带权路径长度：结点与根之间的路径长度与该结点上权的乘积

  • 树的带权路径长度（树的代价）：树中所有叶子结点的带权路径长度的和

  • 哈夫曼树：树的带权路径长度（树的代价）最小

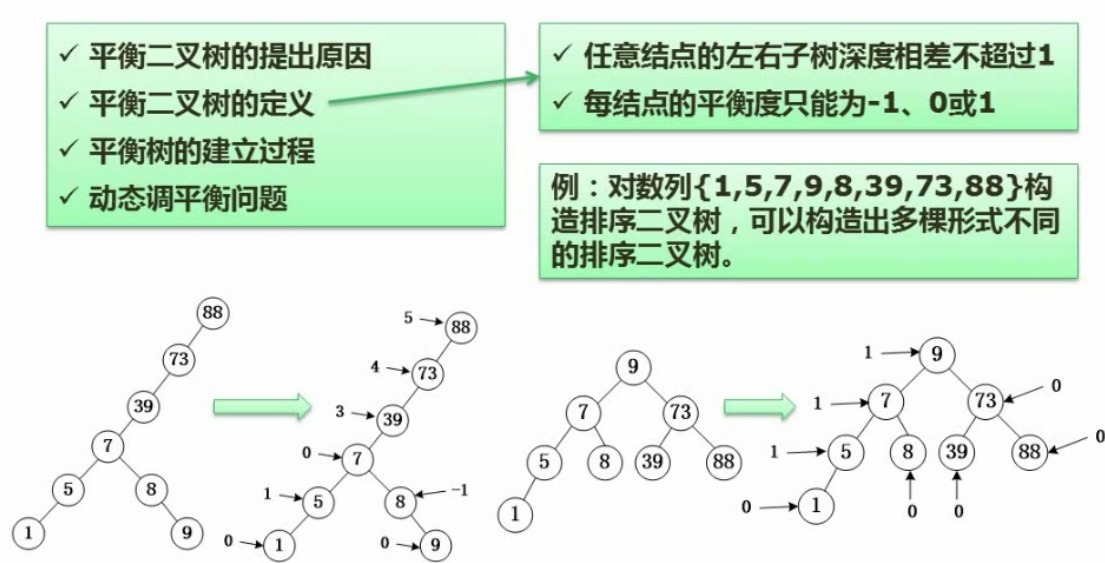
  构造哈夫曼树：依次找权值最小的两个

• 线索二叉树（方便遍历）

  在二叉树基础上增加前驱和后继信息，按前序、中序、后序遍历分为前序线索二叉树、中序线索二叉树、后序线索二叉树

• 平衡二叉树（提高排序二叉树的查找效率）

  任意节点的左右子树深度相差不超过1

  每结点的平衡度（=左子树深度-右子树深度）只能为-1、0、1

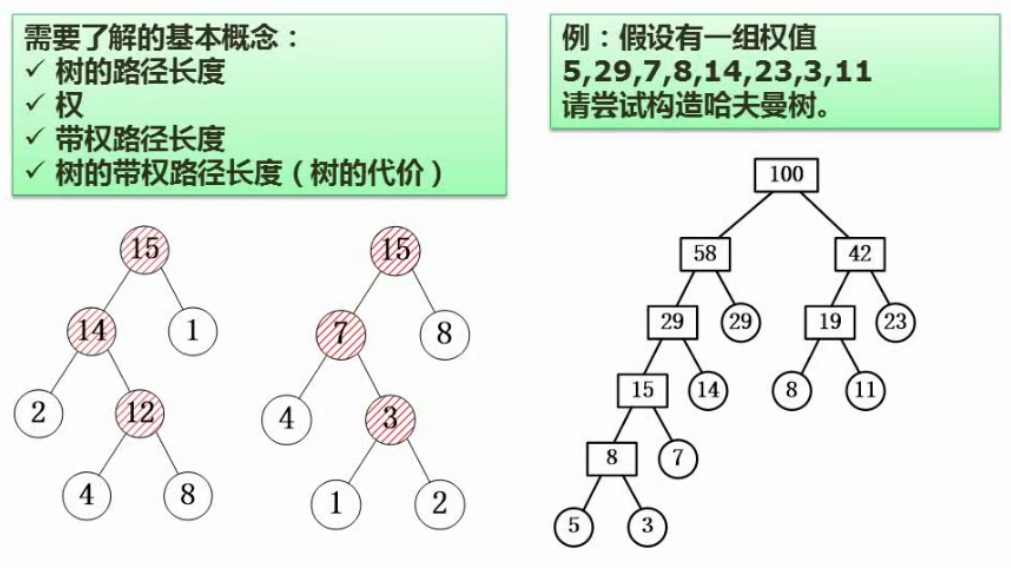
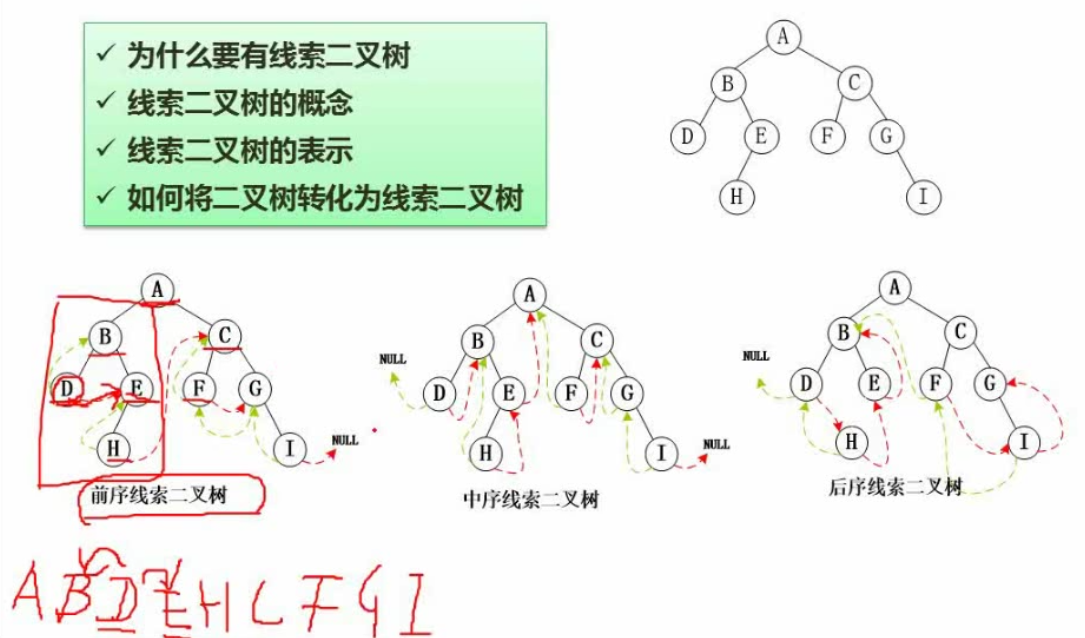
图

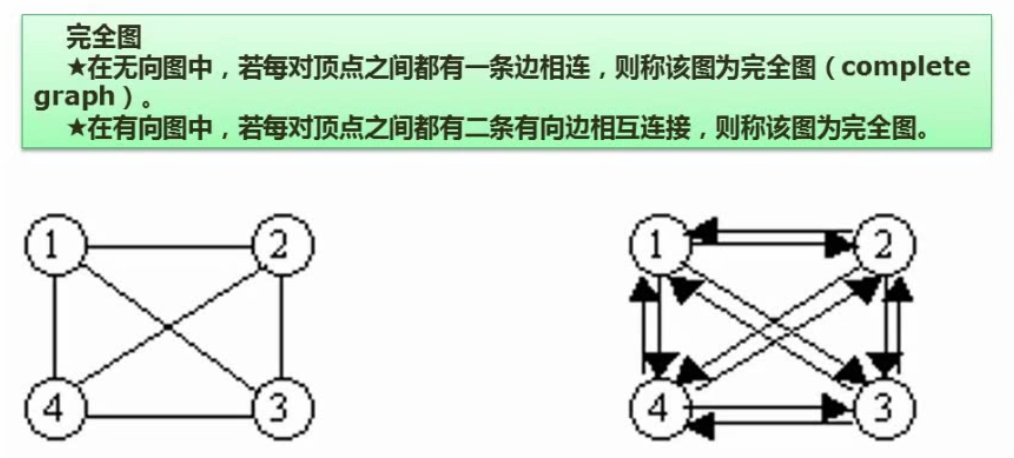
基本概念

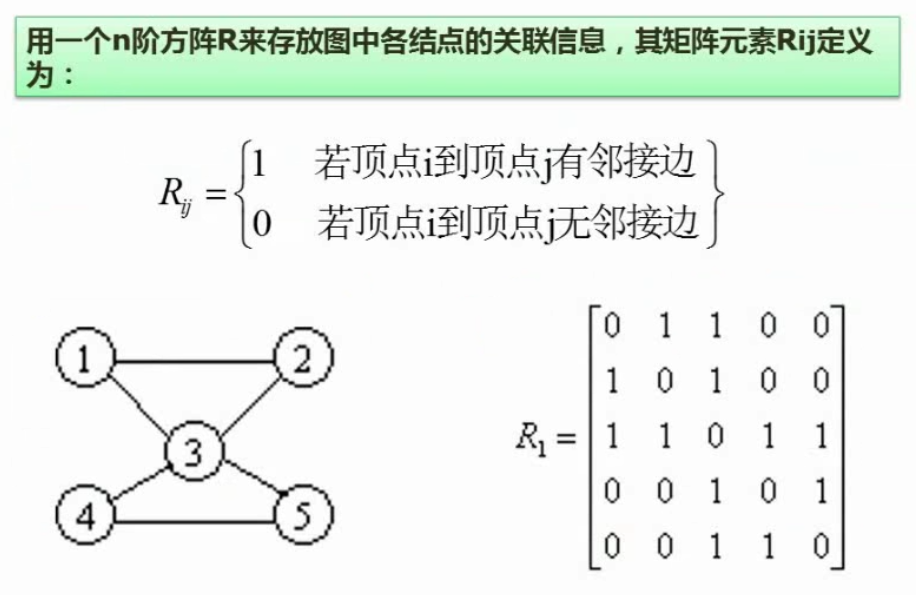
邻接矩阵

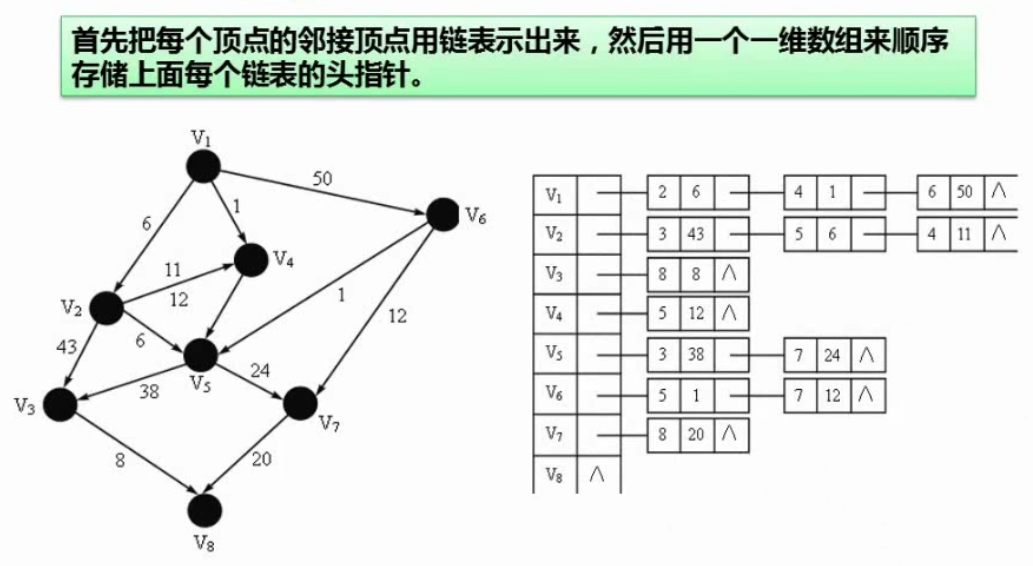
邻接表

图的遍历

• 深度优先遍历

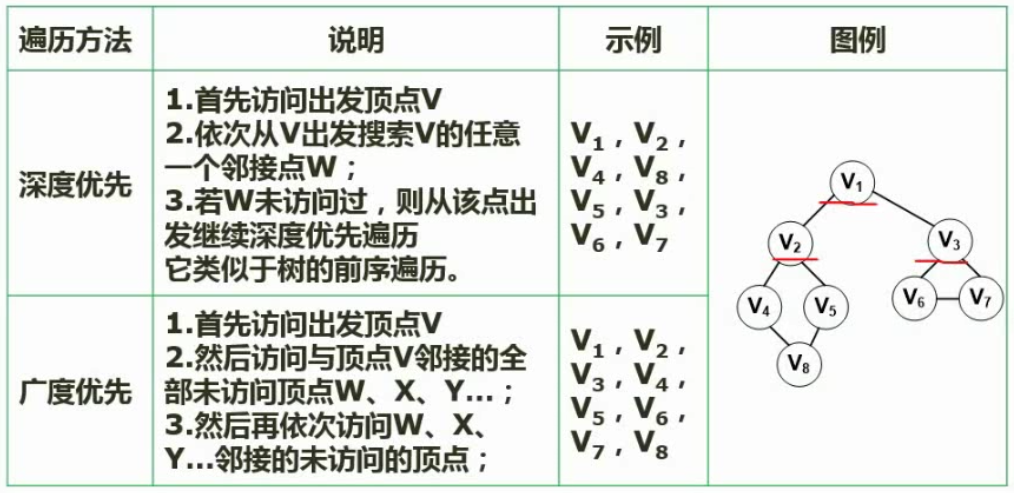
• 广度优先遍历

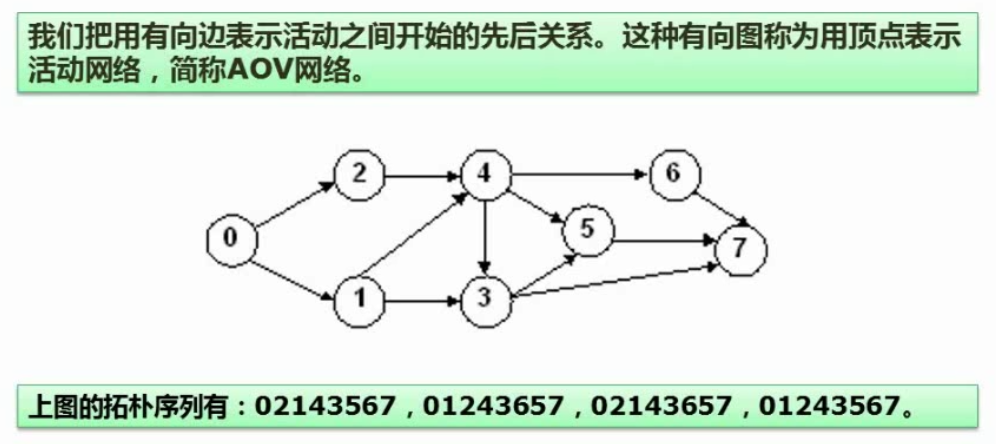
拓扑排序（选择题）

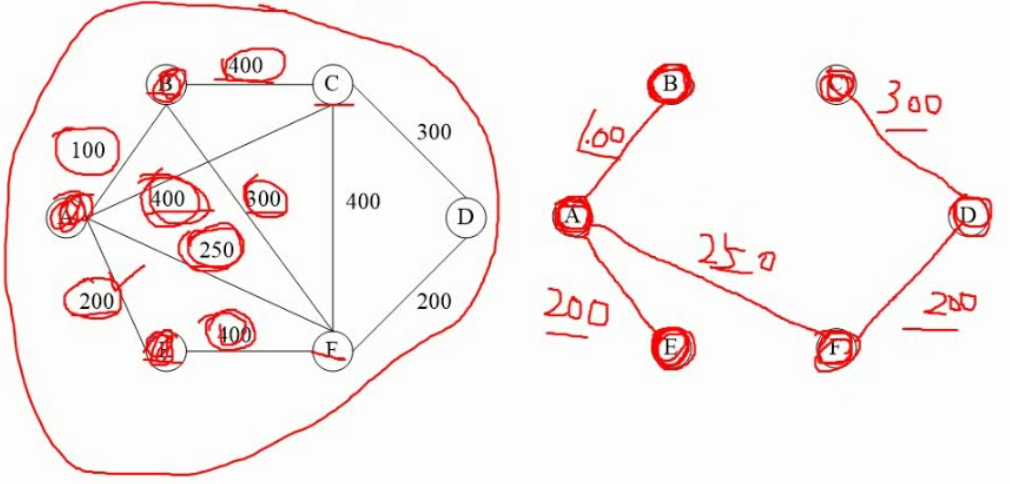
图的最小生成树

• 图和树的最大区别：树没有环路

• 树的结点数/边数 = n/n-1

• 普里姆算法

从一节点开始，选择距离最短的结点（不能选会构成环路的节点）

• 克鲁斯卡尔算法

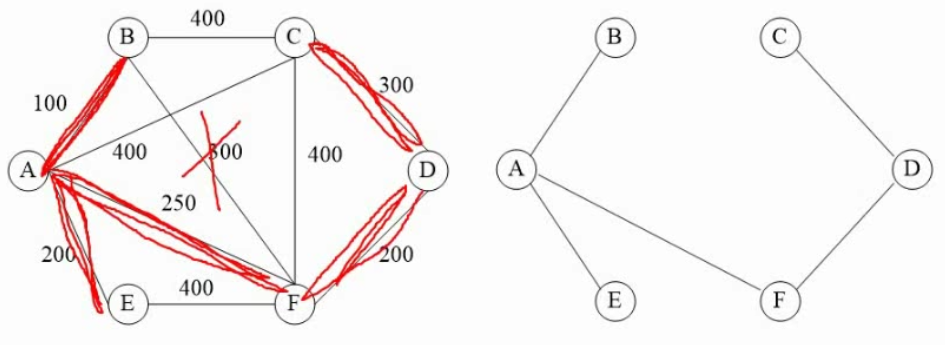
选择不构成环路的最小边

算法基础

算法的特性

• 有穷性：执行有穷步之后结束

• 确定性：算法中的每一条指令都必须有确切的含义，不能含糊不清

• 输入：>= 0

• 输出：>= 1

• 有效性：算法的每个步骤都能有效执行并能得到正确的结果。例如除数为0违反有效性

算法的复杂度

时间复杂度（必考，多在下午）

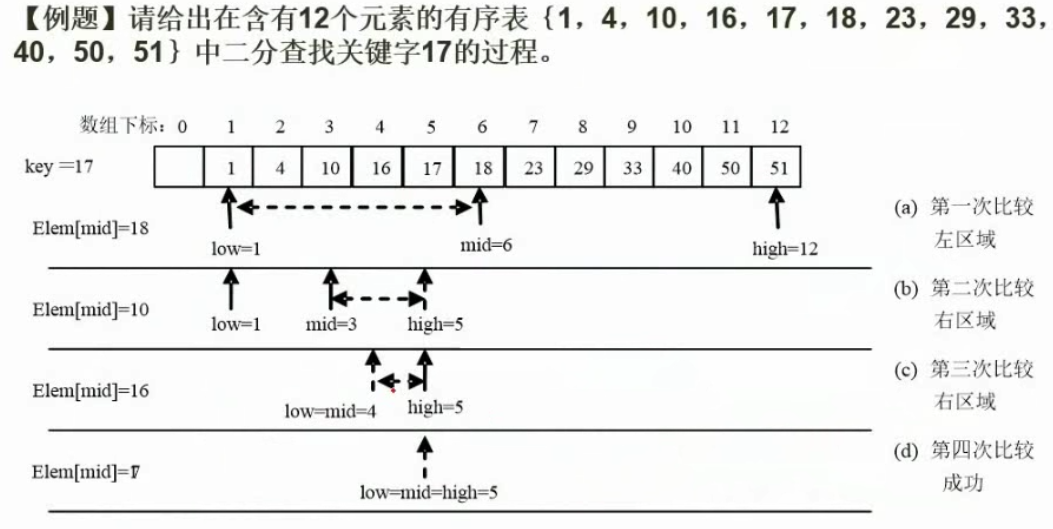
查找算法

• 顺序查找（时间复杂度O(n)）

• 二分查找（有序排列才能用，小数取整，时间复杂度O(log₂n)）

• 散列表

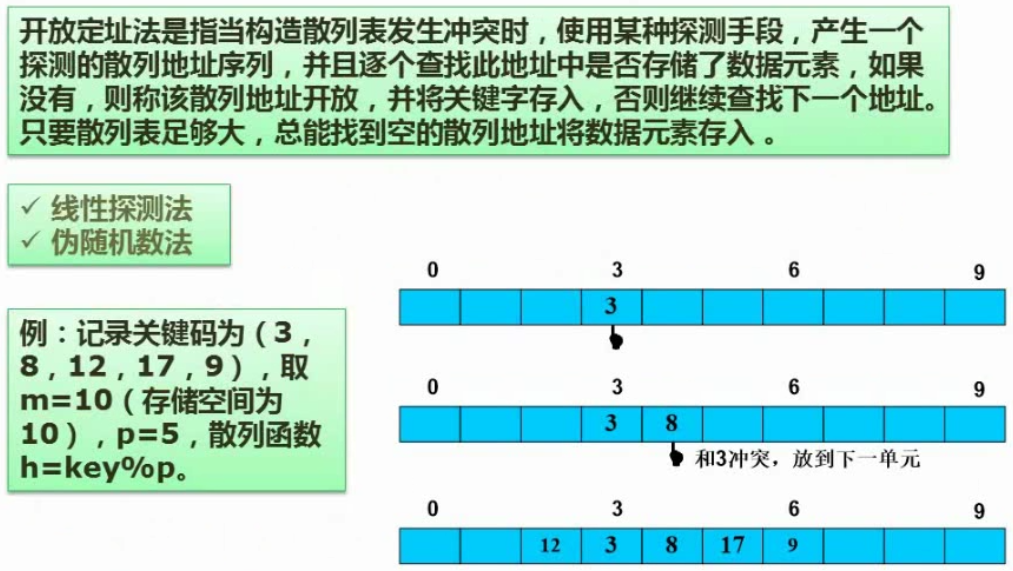
散列冲突的解决：线性探测法、伪随机数法

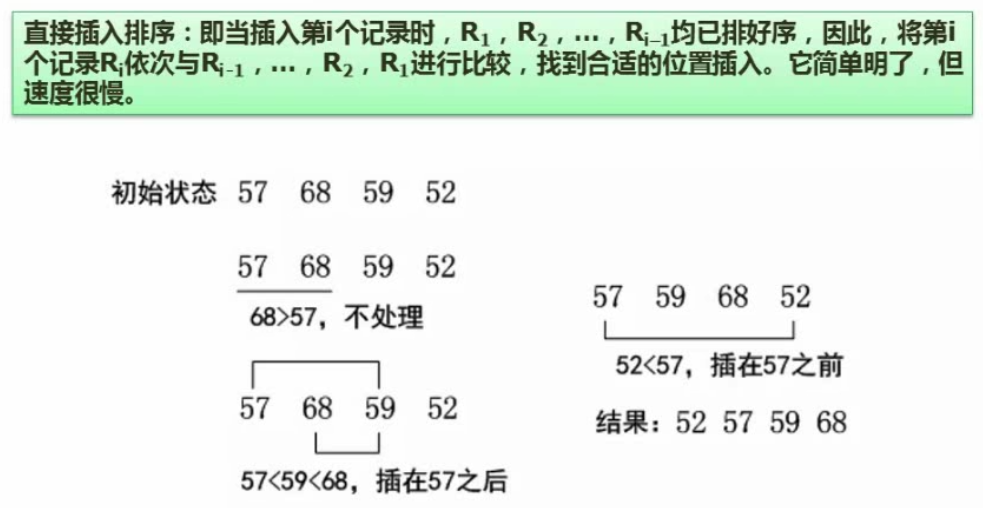
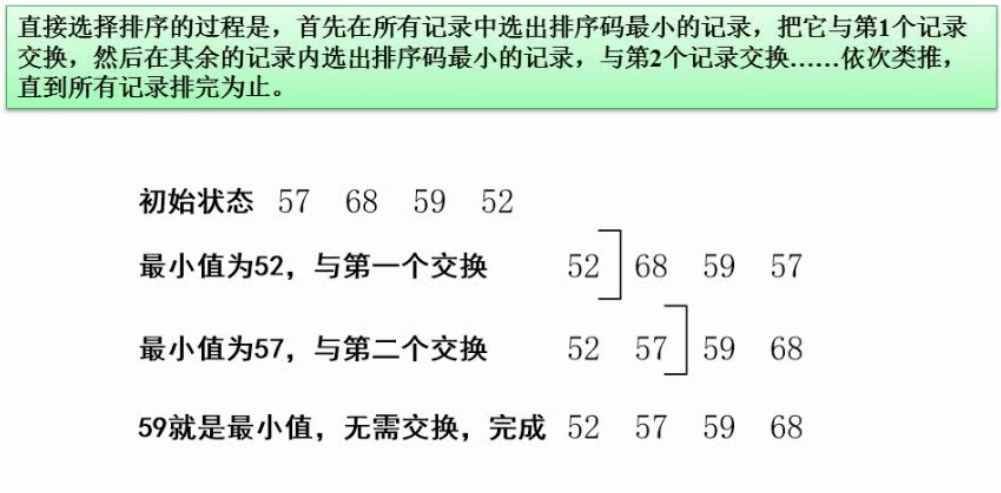
排序算法（必考）

• 直接插入排序（数据越多，效率越低）

• 希尔（Shell）排序（减少比较次数）

• 直接选择排序

• 堆排序（最复杂，效率比直接选择高，更适用于部分排序，如求前三名）

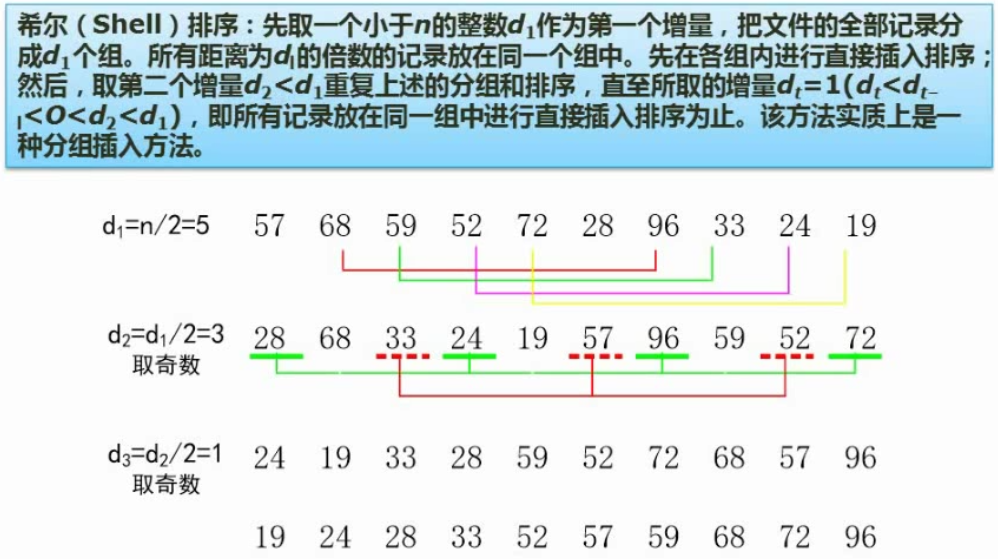
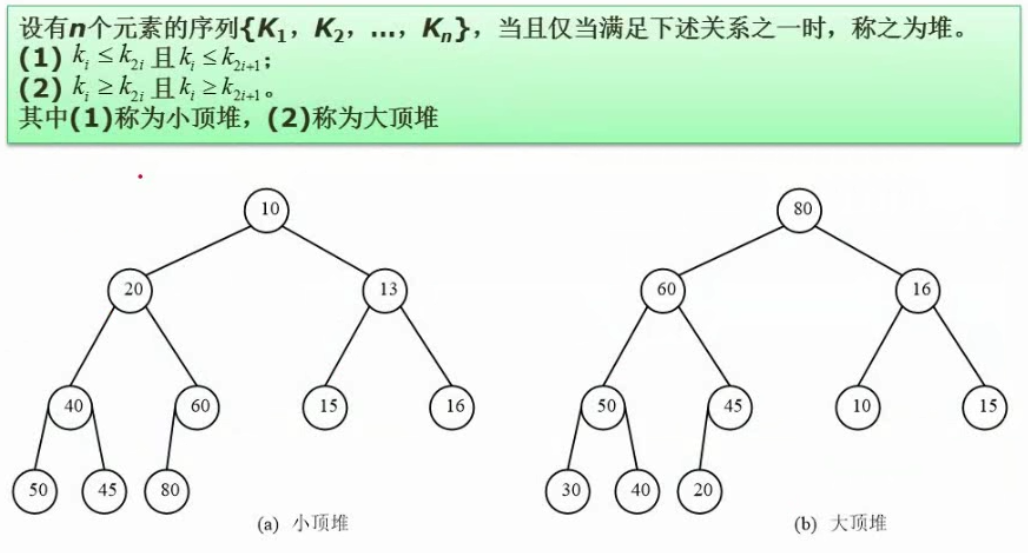
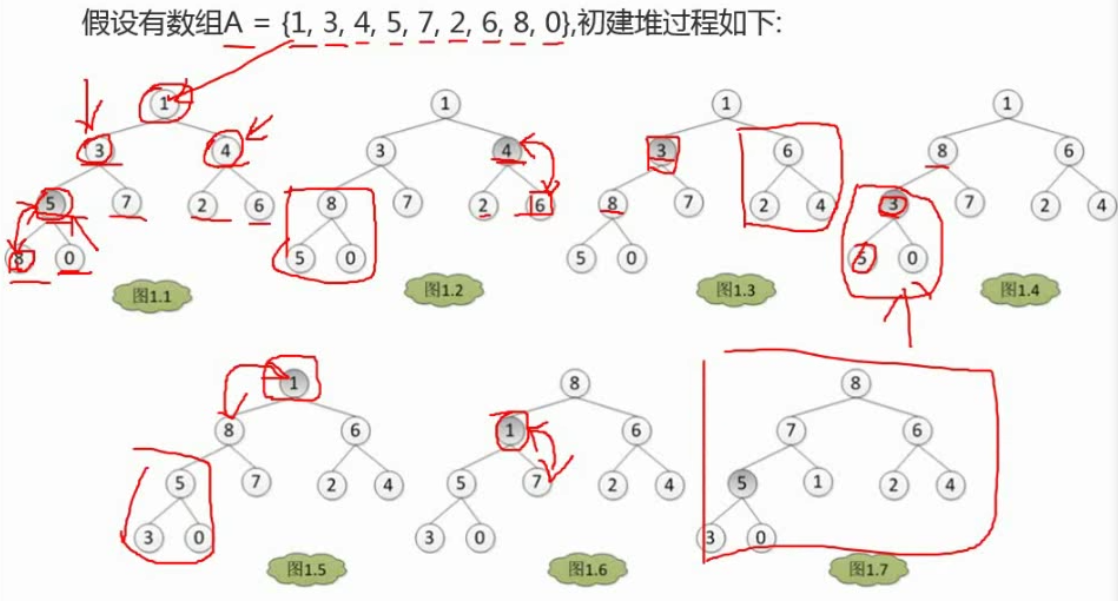
初建堆：按完全二叉树排列，从最后一个非叶子结点开始进行多次调整

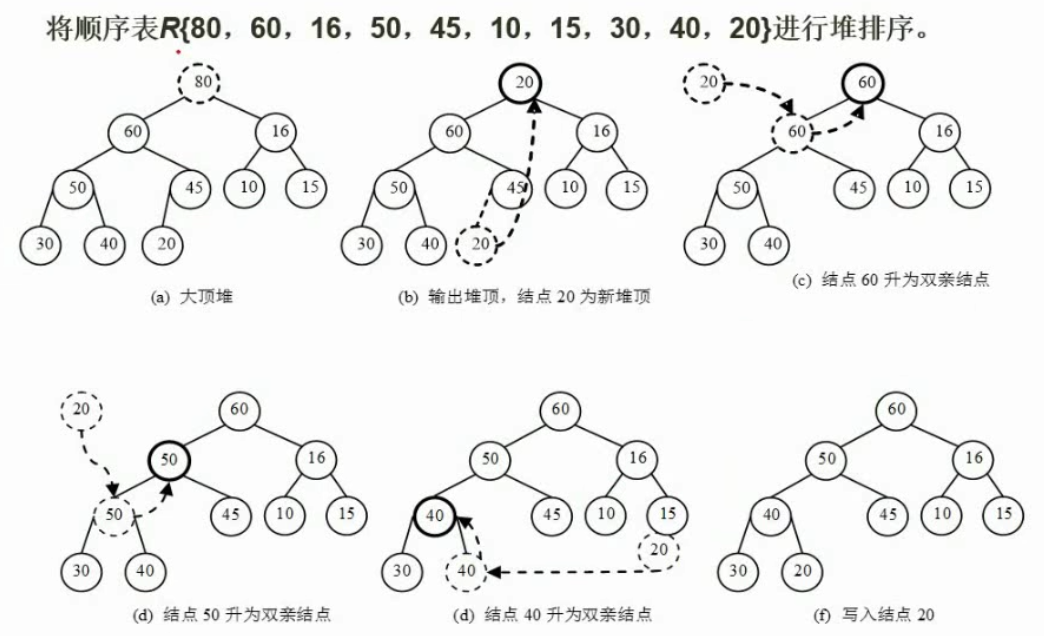
堆重建：取出堆顶元素，将最后一个结点作为新堆顶再次进行多次调整

• 冒泡排序

• 快速排序（递归）

• 归并（合并）排序

• 基数排序

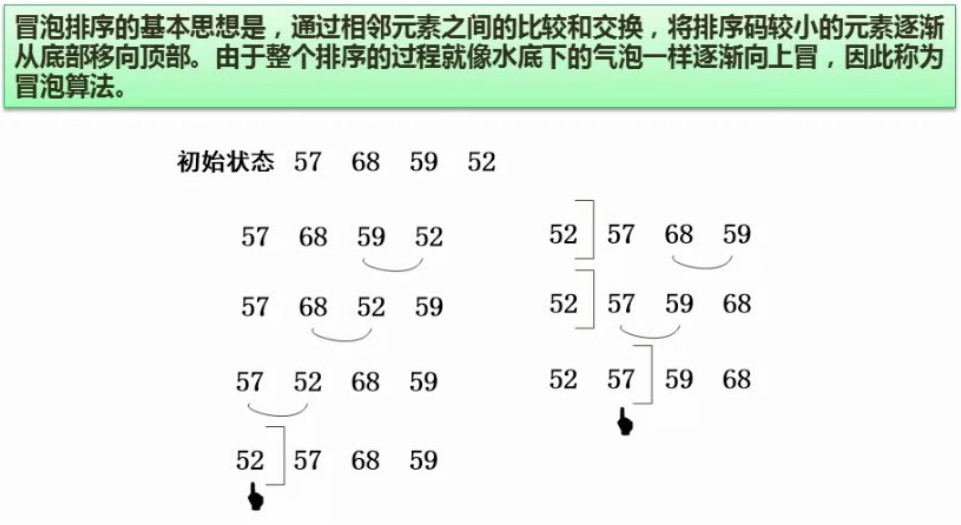
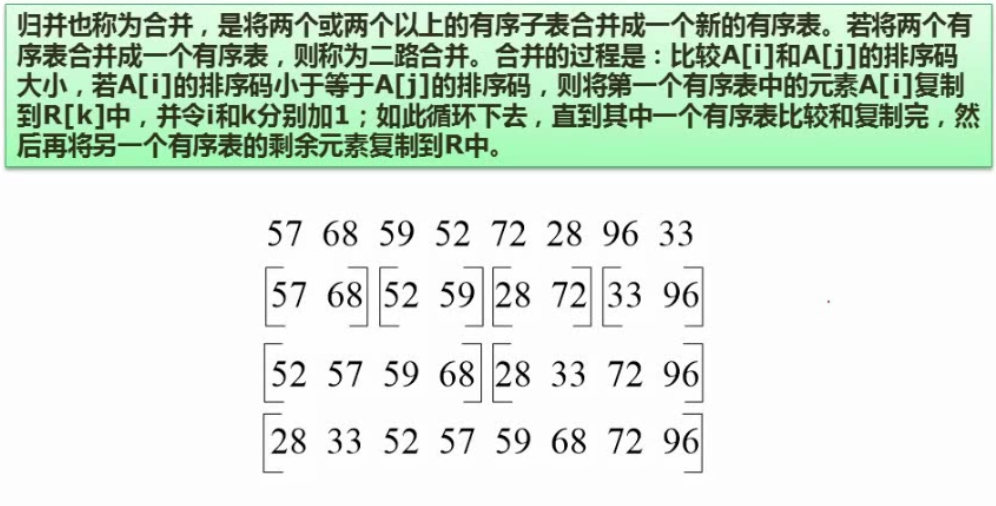
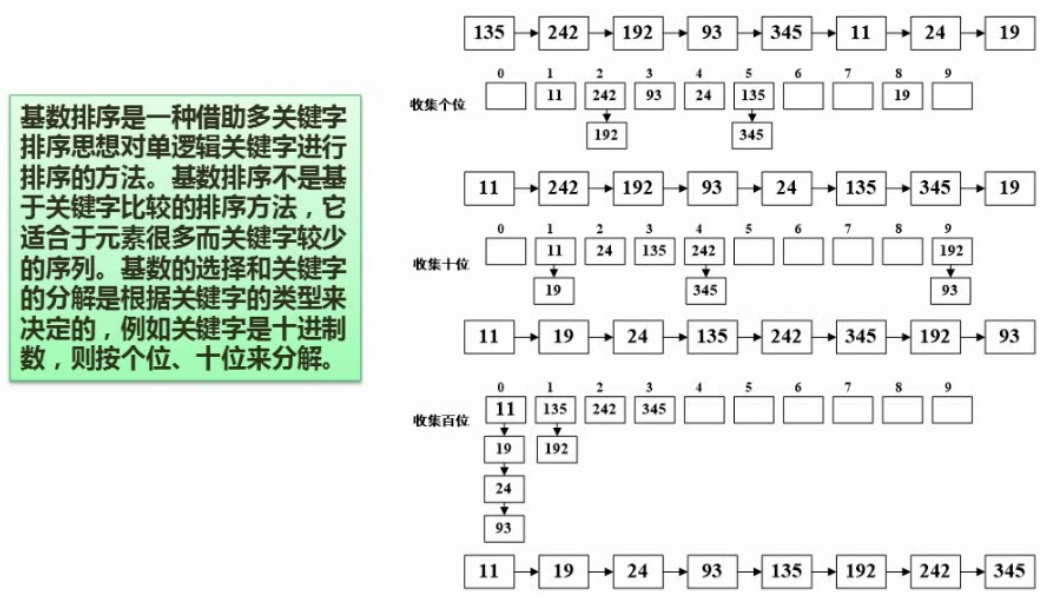
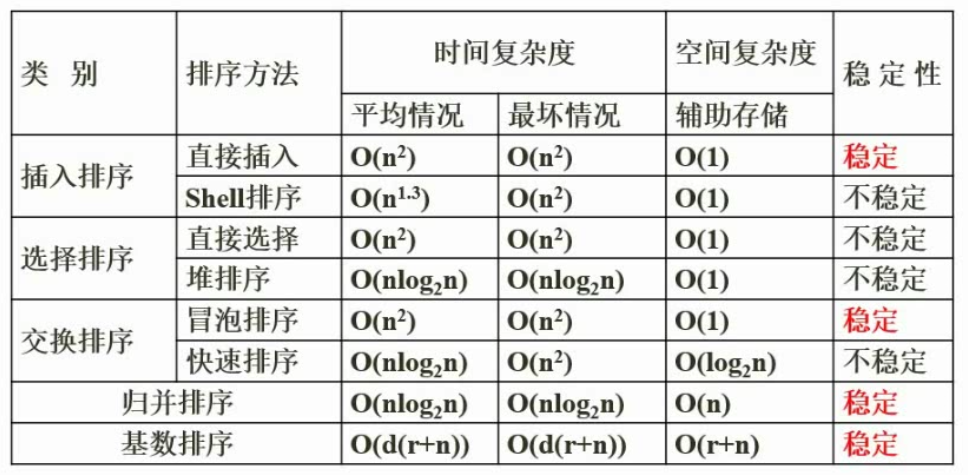
排序算法的时间复杂度、空间复杂度及稳定性（常考）